Um quilo de dióxido de carbono a é comprimido de a em um dispositivo pistão-cilindro arranjado para executar um processo politrópico . Determine a temperatura final tratando o dióxido de carbono como (a) um gás ideal e (b) um gás de van der Waals.
Passo 1
Okay galera, vamos lá! O dióxido de carbono é comprimido num dispositivo de pistão-cilíndrico num processo politrópico. A temperatura final deve ser determinada utilizando as equações ideais de gás e van der waals. (a) O volume específico no estado inicial é,

De acordo com a especificação do processo,
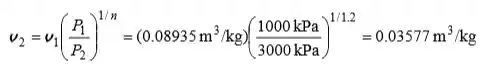
A temperatura final é então,

Passo 2
b) As constantes da equação de van der Waals para o dióxido de carbono são determinadas como,

Aplicando a equação van der Waals ao estado inicial,
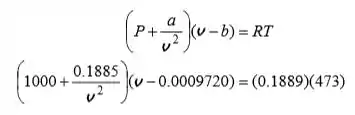
Resolvendo a equação pelo EES nos dá,
![]()
De acordo com a especificação do processo.

Aplicando a equação van der Waals ao estado final,
