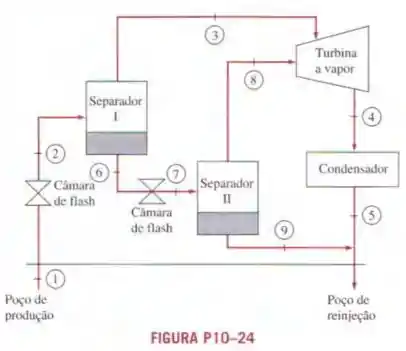
Reconsidere o Problema . Agora, propõe-se que a água líquida que deixa o separador seja conduzida para outro separador de líquido mantido a , e que o vapor produzido seja encaminhado para o estágio de baixa pressão da mesma turbina. Ambos as correntes de vapor saem da turbina no mesmo estado de e de título. Determine (a) a temperatura do vapor na saída do segundo separador de líquido, (b) a potência produzida pelo estágio de baixa pressão da turbina e (c) a eficiência térmica da usina.
Passo 1
Bora lá galera!
Assumindo que existem condições de operação estável e que as mudanças de energia cinética e potencial são desprezíveis.
Então temos que responder 4 alternativas, e por isso vamos começar buscando os dados das tabelas A-4, A-5 e A-6.
- Como o sistema tem várias partes, então vamos lá com calma e paciência :)
- A taxa de fluxo de massa no estágio inferior da turbina é:
- Finalmente o último item dessa questão, em que nos pede para calcularmos a eficiência térmica da usina. Portanto:
A taxa de fluxo de massa de vapor através da turbina é:
Buscando os dados mais uma vez, temos que:
A temperatura do vapor na saída do segundo separador de líquido é .
Uhull !! Primeira etapa concluída com sucesso!
Passo 2
E a potência produzida pelo estágio de alta e baixa pressão da turbina:
Passo 3
Até que enfim, calculamos a eficiência térmica da usina:
Essa questão foi, heim... Bora pra próxima?