Resolva o problema 11.9 para seis partículas indistinguíveis, que obedecem à estatística de F-D. Neste caso
Passo 1
E ae brother do Responde Aí, tá tudo ok?
Hoje vamos resolver mais uma questãozinha de mecânica estatística. Vale lembrar que não é algo muito simples de resolver, mas vamos responder juntinhos para um melhor entendimento, belezinha?

A questão pede para calcularmos as propriedades do macroestado do sistema, como a probabilidade estatística e o número de ocupação do estado de energia. Mas para isso precisamos utilizar alguma estatística, porém a questão nos pede para realizar a questão utilizando a estatística F-E. Que é a seguinte formulinha:
Lembrando uma coisa, a estatística F-E ela leva em consideração o princípio de exclusão de Pauling, ou seja, cada nível de energia não pode ter mais partículas que a degenerescência que é .
E esse valor vem do exercício 11.9 que, consequentemente, vem do exemplo 11.6, iae sacou?

Passo 2
Primeiramente, para resolver esse tipo de questão precisamos montar os níveis de energia, mas como montar isso?
Cara é chatinho, mas precisa desenhar, é a forma mais concreta de fazer esse negócio.
A questão nos informa que temos 8 níveis de energia e a energia total de um macroestado precisa ser , portanto, começando no 0 teremos a linha do 0 e depois teremos uma linha para cada nível gerando 8 níveis de energia. Ficando assim:
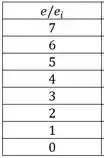
Nomeando os níveis de energia por para ficar mais bonitinho na tabela. Para desenhar, cada um faz do seu jeito. Eu faço assim, eu coloco tudo no estado fundamental e vou distribuindo ao longo dos níveis até ficar com a energia que é 7. Aí temos que no primeiro nível por exemplo fica assim:
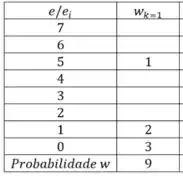
Veja que o nível mais alto é o 5, para o primeiro estado. Para o segundo estado eu coloco 3 partículas no estado fundamental o 0, e vou distribuindo de uma forma que fique diferente do anterior. Depois de realizar isso inúmeras vezes o meu fica:
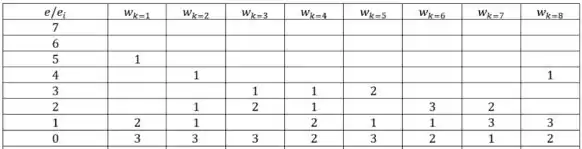
E essa é nossa distribuição de energia, sacou? Bora, para os próximos passos.
Passo 3
Para os próximos passos, precisamos calcular o número total de microestados que é dado pela seguinte fórmula:
E vamos aplicar essa formulinha em cada macroestado. Temos que, para o primeiro macroestado, existe Partícula no nível 5, 2 no nível 1 e 3 no nível 0. Portanto, temos que:
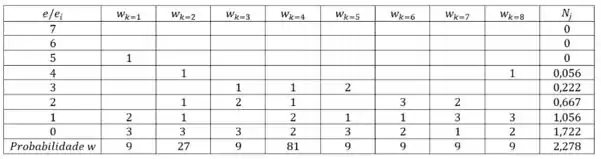
Realizando para os próximos estados podemos colocar mais uma linha que se chama probabilidade e nossa tabelinha se torna:
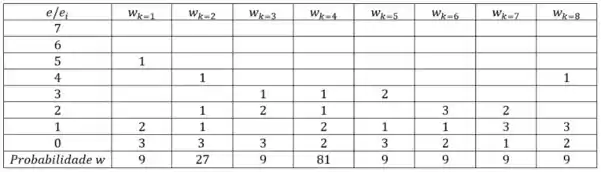
Somando os elementos da linha probabilidade temos que:
Passo 4
Agora precisamos apenas calcular o número de ocupações presente em cada nível de energia e para isso vamos utilizar a seguinte formulinha:
Agora vamos calcular o número de ocupações no 5 nível por exemplo temos 1 partícula no nível 5 com com , com um peso termodinâmico . Portanto:
No demais níveis, temos:
E finalmente terminamos a questão, aqui calculamos todas as proporções de ocupações em cada nível de energia.
Resposta
E calculando tudo geramos a seguinte figurinha: