Enunciado
Termodinâmica - Introdução a termodinâmica da engenharia química, J.M.Smith Van Ness- Ed: 7º - Capítulo 5.Problemas - Ex. 31
Seja o aquecimento de uma casa por um forno, que serve como um reservatório fonte de calor a uma temperatura alta TF. A casa age como um reservatório sumidouro de calor a temperatura T, e uma quantidade de calor IQI deve ser adicionada à casa durante um certo intervalo de tempo para manter essa temperatura. Naturalmente, o calor IQI pode ser transferido diretamente do forno para a casa, como é comum na prática. Entretanto, um terceiro reservatório de calor encontra-se facilmente acessível, a vizinhança, a uma temperatura Tu, que pode servir como outra fonte de calor, assim reduzindo a quantidade de calor necessária a partir do forno. Com TF = 810 K, T = 295 K, Tu= 265 K e IQI = 1.000 kJ, determine a quantidade mínima de calor IQi:J que deve ser extraída do reservatório fonte de calor (forno) a TF. Nenhuma outra fonte de energia encontra-se disponível.
Passo 1
Fala galerinha tranquilidade, seguinte como temos dois reservátorios vamos entender o que está acontecendo:
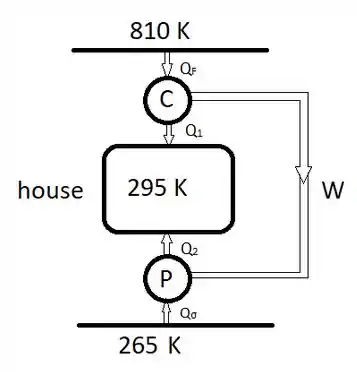
Passo 2
Como nós estamos utilizando duas fontes, a máquina mais eficiente que trabalha entre duas fontes é a de Carnot, sabendo disso vamos iniciar com a quantidade de calor a se transferir para casa de 1000J:
Conhecendo a equação da máquina de Carnot temos:
Passo 3
O passo 2 nos forneceu 5 equações e cinco incógnitas, que nós leva a fazer algumas manipulações algebricas para compreender o que está acontecendo:
Agora reorganizando as equações com a parte do calor ficamos:
Com isso podemos dizer que o trabalho da bomba é igual ao trabalho da máquina resultando:
Resposta
Utilizando a equação da máquina de Carnot, para o calor da fonte podemos encontrar:
