Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 14.Problemas - Ex. 78
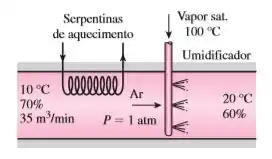
Um sistema de condicionamento de ar opera a uma pressão total de 1 atm e consiste em uma seção de aquecimento e um umidificador que fornece vapor úmido (vapor de água saturado) a 100 °C. O ar entra na seção de aquecimento a 10 °C e 70% de umidade relativa a uma taxa de , saindo da seção de umidificação a 20 °C e 60% de umidade relativa. Determine
- a temperatura e a umidade relativa do ar quando ele sai da seção de aquecimento,
- a taxa de transferência de calor da seção de aquecimento e
- a taxa com a qual a água é adicionada ao ar na seção de umidificação.
Passo 1
Vamos assumir que:
Este é um processo de fluxo constante e, portanto, a vazão mássica do ar seco permanece constante durante todo o processo ().
Ar seco e vapor de água são gases ideais.
As mudanças de energia cinética e potencial são insignificantes.
Os estados de entrada e saída do ar são completamente especificados e a pressão total é de 1 atm. As propriedades do ar em vários estados são determinadas a partir da tabela psicrométrica (Figura A-31) como
Passo 2
Na letra a, a quantidade de umidade no ar permanece constante, flui através da seção de aquecimento (, mas aumenta na seção de umidificação (. O caudal mássico do ar seco é
Observando que Q = W = 0, o balanço de energia na seção de umidificação pode ser expresso como
Resolvendo para achar :
Assim, na saída da seção de aquecimento, temos de ar seco e de ar seco, o que fixa completamente o estado. Então, a partir do gráfico psicrométrico, lemos:
Passo 3
Na letra b, a taxa de transferência de calor para o ar na seção de aquecimento é
Passo 4
E na letra c, a quantidade de água adicionada ao ar na seção de umidificação é determinada a partir da conservação da equação de massa de água na seção de umidificação,