Um tanque rígido isolado com volume de se encontra conectado por uma válvula a uma linha de alimentação de grande diâmetro que transporta ar a e . O tanque está inicialmente evacuado. O ar escoa para o interior do tanque até que a pressão seja . Utilizando o modelo de gás ideal com razão de calores específicos constante, represente graficamente a temperatura do tanque, em , a quantidade de massa no tanque, em , e a quantidade de entropia gerada, em , em função da pressão em .
Passo 1
Opa, beleza?
Bora resolver essa questão juntos!
Começamos o nosso problema aplicando um balanço de massa para o volume do tanque como o volume de controle:
Como o tanque não tem outros “furos” para o gás escapar e inicialmente o tanque é evacuado, podemos afirmar que:
Assim, o nosso balanço de massa se reduz a:
Aplicando um balanço de energia para o volume do tanque como o volume de controle:
Como o nosso tanque é rígido e bem isolado:
Assim, o nosso balanço de energia se torna:
Abrindo essa equação:
Com :
E :
Passo 2
Para um gás ideal, a energia interna específica é dada por:
E a entalpia específica:
Assim, a nossa equação do Passo 1 se torna:
Para o ar, temos que e o enunciado nos proporciona :
Passo 3
Aplicando a equação dos gases ideais no tanque:
Aplicando :
Fazendo :
Substituindo os dados:
Passo 4
Como o processo não envolve nenhuma transferência de calor ou trabalho, podemos calcular a entropia gerada utilizando a seguinte equação:
Com:
E
Então:
Substituindo na nossa equação:
Substituindo os dados:
Para , ou seja , obtemos:
Passo 5
Para um intervalor , podemos plotar os seguintes gráficos:
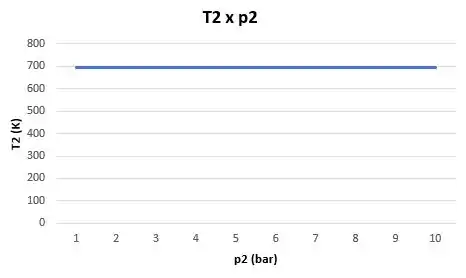
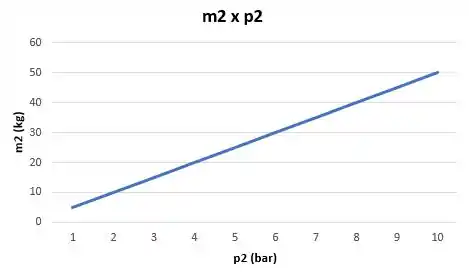
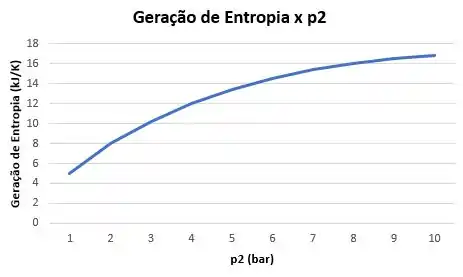
E assim a gente finaliza a nossa questão!
Até a próxima!