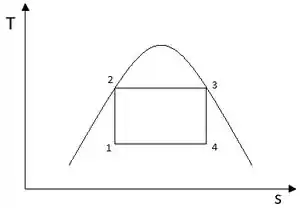
Os trabalhos líquidos e as eficiências térmicas do ciclo de Carnot e do ciclo de Rankine simples ideal devem ser calculados e comparados. Em ambos os casos o vapor d’água entra na turbina a como vapor saturado e a pressão no condensador é de No ciclo de Rankine, o estado na saída do condensador é líquido saturado e no ciclo de Carnot o estado na entrada na caldeira é líquido saturado. Desenho os diagramas de ambos os ciclos.
Passo 1
Bora lá galera!
Vamos começar buscando os dados das tabelas de vapor (Tabelas A-4, A-5 e A-6):
Com os dados que buscamos, conseguimos calcular o :
Show! Agora calculamos o da seguinte maneira:
Agora vamos ver os dados nas tabelas novamente:
Assim,
E finalmente, a eficiência:
CICLO RANKINE
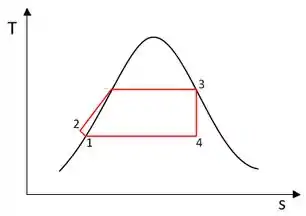
Uhull !! Primeira etapa concluída com sucesso!
Passo 2
Agora para o ciclo de Carnot, buscando os dados das tabelas mais uma vez, temos que:
Assim,
E finalmente, a eficiência:
CICLO CARNOT
Essa questão foi, heim... Bora pra próxima?
Resposta
Rankine:
Carnot:
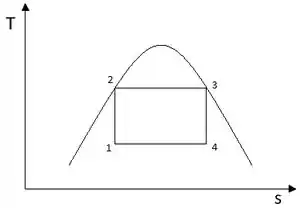
CICLO RANKINE
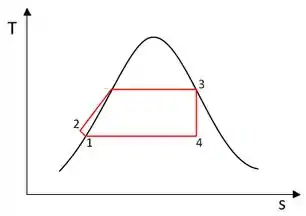
CICLO CARNOT