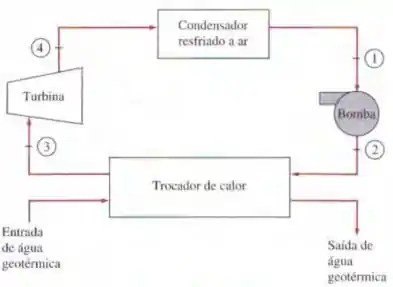
Uma usina de potência utiliza água geotérmica a como fonte de calor. O ciclo opera no ciclo de Rankine simples com isobutano como fluido de trabalho. O calor é transferido para o ciclo por um trocador de calor no qual a água líquida geotérmica entra a a uma vazão de e sai a . O isobutano entra na turbina a e a uma vazão de e sai a e . O isobutano é condensado em um condensador resfriado a ar e bombeado até a pressão do trocador de calor. Assumindo que a bomba tenha uma eficiência isoentrópica de determine (a) a eficiência isoentrópica da turbina, (b) a potência líquida produzida pela usina e (c) a eficiência térmica do ciclo.
Passo 1
Bora lá galera!
Nesse caso temos o ciclo simples de Rankine com o isobutano como o funcionamento
fluido e com isso, assume-se que existem condições de operação estável e que as mudanças de energia cinética e potencial são desprezíveis.
Então temos que responder 3 alternativas, e por isso vamos começar buscando os dados. Porém, as propriedades do isobutano não estão disponíveis no livro, logo podemos obtê-los do software EES.
-
E portanto, finalmente conseguimos calcular a eficiência isoentrópica da bomba:
Uhull !! Primeira etapa concluída com sucesso!
Passo 2
- Agora para a bomba, buscando os dados mais uma vez, temos que:
Com os dados que buscamos, conseguimos calcular o :
Show! Agora calculamos o da seguinte maneira:
Assim,
Logo, a potência líquida será:
Passo 2
Logo, finalmente calculamos a eficiência térmica do sistema:
Essa questão foi, heim... Bora pra próxima?