Vapor d'água entra em um bocal convergente a e com uma velocidade desprezível. Se a expansão for isentrópica, qual é a pressão mínima que pode ser atingida nesse bocal e qual é a área da seção transversal de sua garganta nessa pressão para uma vazão de ?
Passo 1
Os cálculos do problema anterior podem ser realizados para uma série de pressões de saída até que uma área de seção transversal mínima seja encontrada. A pressão correspondente é o mínimo que pode ser obtido no bico convergente. Os valores iniciais das propriedades são iguais aos do problema anterior.
As interpolações na Tabela F.2 em várias pressões e na entropia dada produzem os seguintes valores:
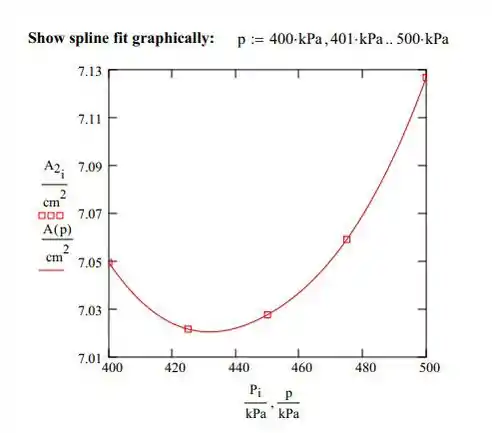
Ajuste os dados P vs. A2 com spline cúbico e encontre o P mínimo no ponto onde a primeira derivada do spline é zero.
(acho)
dados ))