Aplicando os conceitos da primeira e segunda derivadas. Qual o gráfico da função definida em por ?
(a)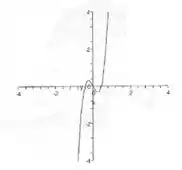
Passo 1
Beleza, o primeiro passo para identificar gráficos de funções (quase sempre) é ver os pontos em que os gráficos cruzam os eixos, porque são os mais fáceis de verificar.
A função não tem uma constante, então não deve cruzar o eixo . De fato, nenhum dos gráficos cruza o eixo, então isso não ajuda por enquanto.
Passo 2
Agora vamos pensar nos pontos onde ela cruza o eixo (ou seja, as raízes do polinômio). Esses pontos vão atender essa equação aqui:
Vamos arrumar um pouco isso:
Beleza, tem duas formas de isso dar certo:
A primeira raiz é , e precisamos resolver essa equação do 2° grau para achar a outra:
Beleza, então temos três raízes, ou seja, nosso gráfico tem que cruzar o eixo em três pontos. Com isso já podemos eliminar a terceira e a quarta opção.
Como , só olhando a escala dos eixos, já dá pra perceber que a opção correta é o último gráfico, mas vamos continuar para demonstrar como usar derivadas para resolver o problema.
Passo 3
Se procurarmos os pontos com derivada nula:
Ou seja, nos pontos em que , a nossa função tem máximos ou mínimos locais. Vamos substiuir os pontos na função:
Então o gráfico que estamos procurando tem extremos nos pontos e , que é exatamente o que vemos no último gráfico!
Resposta
Letra (e).