Em cada item a seguir, esboce o gráfico de uma função f que satisfaz a todas as condições dadas.
para todo .
para todo .
Passo 1
Olá meu amigo, Yuri aqui e agora iremos esboçar alguns gráficos. O gráfico que iremos esboçar é de uma função que tanto sua primeira derivada quanto a sua segunda derivadas são negativas para todo real. Uma função que satisfaz as condições dadas é:
Essa função tem absolutamente todas as suas derivadas negativas. Agora o que nos falta é gerar o seu gráfico
Passo 2
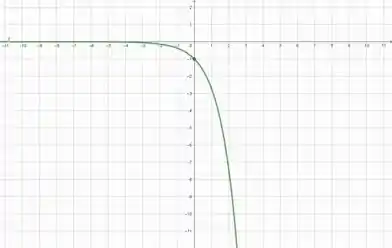
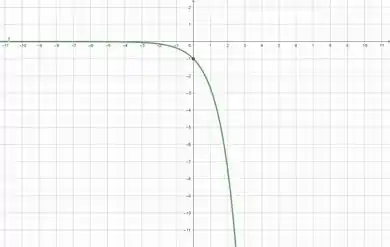
Resposta
Ver o desenvolvimento