4) Considere a função , sendo suas derivadas primeira e segunda dadas, respectivamente, por e . Siga o roteiro abaixo para esboçar um gráfico de :
- Encontre as raízes de
- Encontre as assíntotas horizontais e verticais de , caso existam
- Identifique os intervalos onde é crescente e decrescente
- Encontre os pontos de máximo e mínimo locais de caso existam
- Identifique os intervalos onde é côncava para cima ou para baixo, e encontre os seus pontos de inflexão, caso existam
- Com base nas informações acima, esboce um gráfico de
Passo 1
Passos I e II
Bora lá seguir o roteirinho então. Pelo menos a gente poupa tempo com as derivações. Primeiro vamos ver as raízes:
Como denominador não influencia pra zerar a função, basta fazer:
Opa! Um polinômio de segundo grau! Seja então:
Onde:
Achamos as raízes do polinômio seguindo fórmula de Bháskara, dada por:
Calculando as raízes então, temos:
As raízes vão ser então e . Agora, quando falamos de assíntotas, temos que ver os limites. Bora começar pelas horizontais:
Opa, indeterminação. Mas relaxa, saímos dela com regra de L’Hospital molinho. Derivando em cima e em baixo então, temos:
Agora pro outro limite, temos:
O que também sai por L’Hospital. Sendo assim:
Então nesse caso, não temos assíntotas horizontais! Agora bora ver as verticais. Pra cehcar elas, temos que considerar os limites laterais para valores de que “dão problema” na função. Sendo a função:
Essa função só “dá problema” em porque zeraria o denominador. Fazendo os limites laterais:
Já que os limites explodiram então temos sim uma assíntota vertical em
Passo 2
Passos III e IV
Esses dois passos usam a primeira derivada, então bora fazer eles juntos. A primeira coisa a fazer é fazer uma análise de sinal para:
Como pra ver a raiz da primeira derivada não precisamos do denominador, basta fazermos:
O Que é verdade quando e . Vamos então analisar o sinal da primeira derivada em intervalos que envolvam esses pontos críticos. São eles:
Pro primeiro intervalo, podemos testar , e logo:
Pro segundo, podemos testar , e logo:
E pro terceiro, podemos testar , e logo:
Sendo assim, chegamos a conclusão que a função é crescente em e decrescente em . Afinal, se a primeira derivada é positiva, a função é crescente, se negativa, decrescente. Como a função, antes de cresce e depois decresce, então é um ponto de máximo e como a função, antes de decresce e depois cresce, então é um ponto de mínimo.
Passo 3
Passos V
Agora temos que fazer a mesma análise, beleza? Só que pra segunda derivada. Vamos ter:
Opa, não tem como zerar a segunda derivada! É, realmente não tem, mas veja que:
Como a concavidade é pra cima quando a segunda derivada é positiva, vamos ter concavidade pra cima no intervalo . Como a concavidade é pra baixo quando a segunda derivada é negativa, vamos ter concavidade pra baixo no intervalo . Logo, é o único ponto de inflexão.
Passo 4
Passos VI
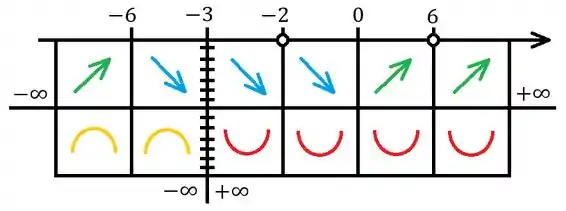
Fechamos viu? Só esboçar tudo. Antes disso, talvez seja uma boa ideia fazer um quadro auxiliar pra juntar todas as informações que achamos até agora. Saca só como fica:
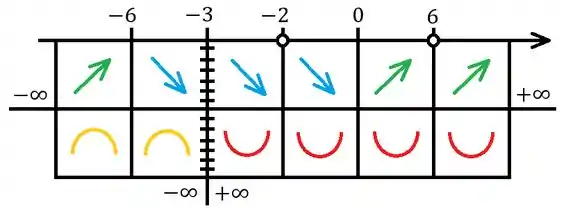
Significados do quadro:
- Eixo superior Eixo demarcado com os pontos encontrados no cálculo das raizes e nos testes da primeira e segunda derivada
- Eixo do meio Mostra a esquerda o resultado do limite para e a direita o resultado do limite para .
- Eixo vertical tracejado Representa a assíntota vertical. A direita e a esquerda do eixo tem os limites laterais calculados.
- Bolinhas brancas Raízes
- Setas pra cima e verdes em qual intervalo é crescente.
- Setas pra baixo e azuis, em qual intervalo é decrescente.
- Curva vermelha em qual intervalo é côncava pra cima.
- Curva laranja em qual intervalo é côncava pra baixo.
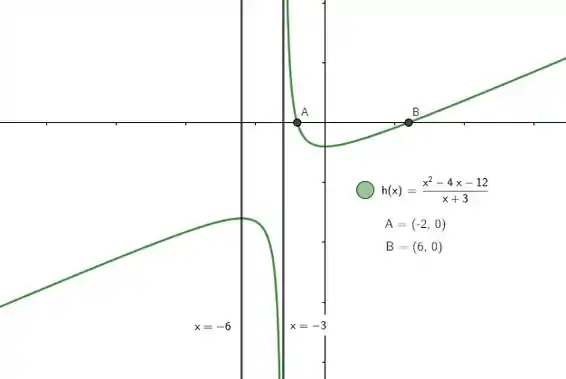
Com o quadro montado, temos um resumo muito bom pro esboço, que deve sair parecido com:
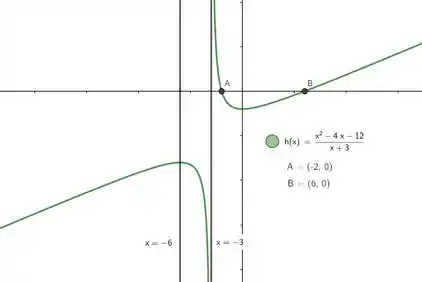
Resposta