Considere a função
cujas derivada e derivada segunda são dadas por:
- Calcule o domínio de definição de .
- Calcule as interseções do gráfico de com os eixos coordenados caso existam.
- Calcule os limites de no infinito e ache as assíntotas horizontais e verticais ao gráfico de caso exista.
- Identifique os pontos críticos, os extremos relativos e os intervalos onde a função é crescente e onde é decrescente.
- Identifique os pontos de inflexão da função e os intervalos de concavidade para cima e para baixo.
- Usando as informações anteriores, faça um esboço do gráfico de .
Passo 1
Ufa! Se o enunciado já é grande, imagine a resolução. Ajeita a poltrona aí e vamos lá!
(a)
Essa aqui é bem fácil. A restrições ao domínio, para funções racionais como é o caso do nosso amigo , ocorrem quando o denominador zera. Mas, nesse caso, o polinômio do denominador não tem raízes reais e, portanto, nunca zera . Assim podemos concluir que:
Passo 2
(b)
Essa aqui também tá limonada gelada no verão. Para sabermos quando toca o eixo x, igualamos à zero:
Como para todo , garantimos que:
Veja que, por Bhaskara:
Como , não há raiz real e, portanto, a função nunca encontra o eixo , coitada.
Já para o eixo , igualamos a zero:
Logo, a interseção ocorre no ponto .
Passo 3
(c)
Vamos calcular o limite no infinito:
Dividindo tudo pelo monômio de maior grau:
Jogando os limites para dentro da fração:
De maneira análoga:
Assim, como essa é a definição do cálculo da assíntota horizontal e o limite existe, temos uma assíntota na reta:
E quanto as assíntotas verticais? Elas só aparecem quando existe algum ponto de indeterminação na função. Como a função tem domínio em todos os números reais, isso não vai acontecer e não existem assíntotas verticais nesse problema.
Passo 4
(d)
Só para não ter que ir lá em cima e voltar:
Os pontos críticos ocorrem quando a derivada não existe ou é zero. Como denominador não zera nunca (sem raízes reais), só nos resta calcular os pontos onde a derivada é zero:
Uma vez que para todo , garantimos que:
Ou seja, temos dois pontos críticos. Um em e o outro em .
Agora, vamos ver quando a função é crescente e descrecente. Ela será crescente quando e decrescente do contrário.
Dessa maneira, precisamos testar o sinal da derivada. Ele pode mudar, e só vai mudar, ao passar por um ponto crítico, então vamos analisar valores entre cada um dos pontos.
Temos também que o denominador não muda de sinal, é sempre positivo, então só precisamos analisar o sinal do numerador.
Sendo e pegando valores para cada região, como
Assim, temos a seguinte tabela:

Ou seja, pelo sinal, concluímos que a função é crescente para e decrescente para ou .
Legal, ainda falta coisa. Falta determinar os máximos e mínimos. Aí entra o teste da primeira derivada. Como a derivada era negativa para valores menores que e positiva para valores imediatamente maiores, temos que esse é um ponto de mínimo.
Do contrário, concluímos que é um ponto de máximo.
Passo 5
(e)
Só para não ter que ir lá em cima e voltar:
Beleza, a função é côncava para cima se e côncava para baixo no contrário. Assim, vamos ter que analisar o sinal da segunda derivada.
O denominador novamente não mudará de sinal, então só precisamos analisar o sinal do numerador. Sendo:
Zerando em:
Só trocará de sinal passando por esses pontos. Então testamos o sinal entre eles:
Em tabela:

Então a função é côncava para baixo para e .
Será côncava para cima para e .
Os pontos de inflexão aparecem quando a função troca de concavidade, ou seja, em:
Passo 6
(f)
Através dos dados, chegamos ao seguinte gráfico:
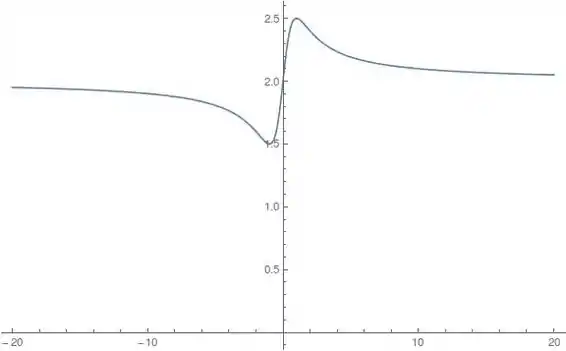
Resposta