Considere a função: .
Indique seu domínio e os interceptos.
Encontre os seus extremos, classifique-os e indique onde a função é crescente ou decrescente.
Indique onde a função tem concavidade para cima ou para baixo e determine seus pontos de inflexão, caso existam.
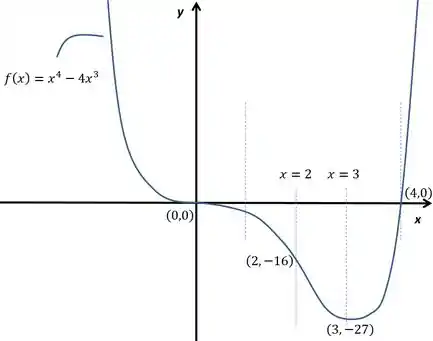
Esboce o gráfico da função.
Passo 1
Bom, é uma função polinimial, então o domínio não tem nada que o complique, certo? Domínio será o conjunto dos reais.
Além disso, pode ser escrita da seguinte maneira:
Ou seja, seus interceptos com o eixo são suas raízes e . Já o intercepto com o eixo , justamente onde , temos .
Sendo assim os interceptos de com os eixos principais são nos pontos e .
Passo 2
Para encontrar extremos e analisar crescimento de temos que olhar para sua derivada:
Nessa situação, os máximos ou mínimos ocorrem quando , o que ocorrerá, de acordo com quando e quando .
Vamos olhar para o sinal dessa derivada, que aparentemente só depende de , uma vez que é sempre positivo: será negativa antes de e positiva quando . Nessa situação, a derivada até será nula em , mas não será um ponto de máximo ou mínimo já que a derivada seria negativa antes e depois desse ponto, não havendo mudança no crescimento.
Assim, temos que é crescente para e decrescente para , sendo um ponto de mínimo, já que sua derivada é decrescente antes e crescente logo depois do ponto.
Passo 3
Concavidade, temos que olhar para a derivada segunda:
Vamos que será nula quando e , serão nossos pontos de inflexão. Como essa derivada segunda é uma parábola de concavidade para cima, ela será negativa entre suas raízes e positiva no resto do domínio.
Assim, temos concavidade para baixo entre e , para cima em e e dois pontos de inflexão nesses mesmos valores de que delimitam o sinal da concavidade.
Passo 4
Bom, agora a questão é juntar tudo o que tiramos de informação nas outras letras e esboçar a curva. Só um detalhe, acontece que não foi pedida a análise das assíntotas, você pode até fazer, mas já te dou um spoiler: não vai achar nenhuma; não há descontinuidades, então não há assíntotas verticais; os limites das definições da assíntota horizontal e da oblíqua explodem, então também não temos dessas.
Enfim, lá vai o esboço, levando em conta que :