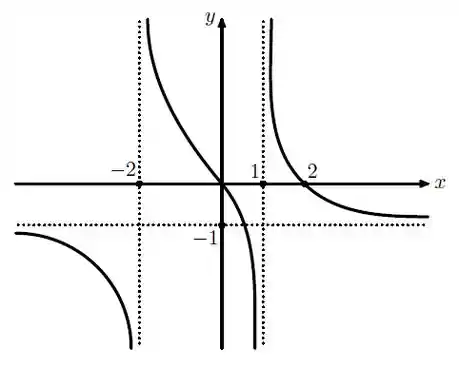
Considere uma função \ com as seguintes propriedades:
- , para todo no domínio da função;
- ;
- para e para ;
- e ;
- e .
Faça um esboço do gráfico dessa função.
Passo 1
Nessa questão de esboço de gráfico todas as informações necessárias já foram dadas, e só cabe a nós interpretá-las.
Então vamos fazer o seguinte: interpretar as propriedades da função uma por uma, beleza?
(a)
“, para todo no domínio da função”
A derivada é sempre negativa, então a função é decrescente em todo o seu domínio. Só isso, vamos pra próxima!
Passo 2
(b)
“”
Bem, aqui não tem muito o que interpretar, simplesmente nos deram os valores da função em 2 pontos. Lembraremos deles na hora de esboçar o gráfico.
Passo 3
(c)
“”
Limites com ?? Isso é sinônimo de assíntota horizontal!
Ou seja, aqui descobrimos que é assíntota horizontal do gráfico da .
Passo 4
(d)
“ para e para ”
Falou em segunda derivada, falou em concavidade! Quando ela é negativa, a função é côncava pra baixo, e quando ela é positiva, a função é côncava pra cima.
Ou seja: tem concavidade pra baixo em , e concavidade pra cima em .
Passo 5
(e)
“ e ”
Aqui temos os limites laterais em , e eles explodem pro infinito. (Aliás, repare que o enunciado diz que não está no domínio da .)
Então isso significa que é uma assíntota vertical do gráfico!
Passo 6
(f)
“ e ”
Aqui é a mesma coisa: outra assíntota vertical em .
Passo 7
Juntando tudo que achamos pela nossa profunda análise interpretativa das propriedades da função, obtemos o seguinte gráfico:
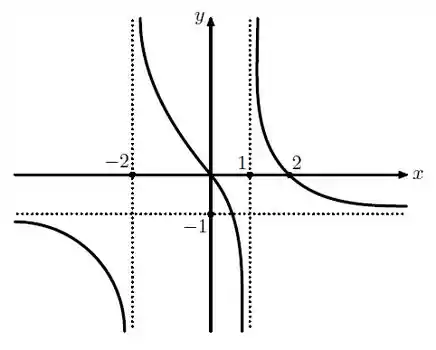
Lindo ele, né? :’)
Resposta