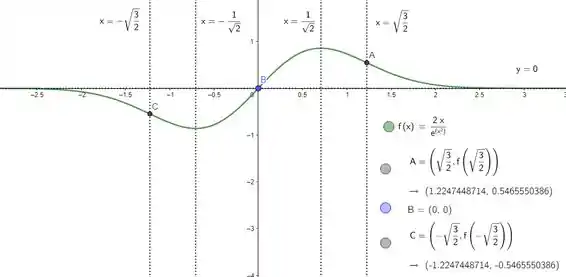
Dada a função , explicite o domínio, intervalos de crescimento e decrescimento, concavidade e pontos de inflexão. Finalmente, esboce o gráfico, indicando os pontos importantes que você encontrou.
Passo 1
Essa questão pede o pacote completo, não é mesmo? Então vamos lá, a começar pelo domínio. Se a gente olhar a função dessa forma:
Vemos que essa função só da ruim se o denominador der , não é mesmo? Mas nesse caso a gente pode ficar tranquilo porque nunca vai ser ! Se nenhum da problema na nossa função, o domínio então vai ser o conjunto dos reais!
Passo 2
Agora vamos ver quando a função cresce e decresce. Pra gente saber isso, temos que ver a inclinação da reta tangente beleza? Se negativa, decresce, se positiva, cresce. E como a primeira derivada da função nos dá a inclinação da tangente, bora derivar:
E agora, bora igualar à pra ver quando a função muda de sinal:
Show, achamos as raízes da primeira derivada. Vamos então checar o que acontece com o sinal da primeira derivada nos intervalos que envolvam as raízes. São eles:
No primeiro intervalo, usando, por exemplo, , temos:
No segundo intervalo, usando, por exemplo, , temos:
No terceiro intervalo, usando, por exemplo, , temos:
Sendo assim, a função vai ser:
Passo 3
Agora vamos falar de concavidades, beleza? É a próxima coisa que a questão pede mesmo! Pra concavidade a ideia é a mesma do passo 2, mas agora vamos usar a segunda derivada. Partiu derivar de novo então:
Ajeitando mais um pouco essa derivada:
Agora sim ta mais bonito. Vamos igualar a então:
Achamos um intervalo em! Mas calma, podem ter outros. Dividindo os dois lados por temos:
Opa, achamos as raízes então da segunda derivada. Agora vamos checar os intervalos que envolvem essas raízes. Se nesse intervalo a segunda derivada for positiva, a concavidade vai ser pra cima. Se for negativa, concavidade pra baixo! Então bora! Os intervalos vão ser:
No primeiro intervalo, usando, por exemplo, , temos:
No segundo intervalo, usando, por exemplo, , temos:
No terceiro intervalo, usando, por exemplo, , temos:
No quarto intervalo, usando, por exemplo, , temos:
Sendo assim, a função vai ser:
E como ponto de inflexão é exatamente o ponto onde a concavidade muda, os pontos de inflexão vão ser:
Como , vamos ter:
Passo 4
Pra gente fechar a questão com chave de ouro, falta só esboçar o gráfico. Mas antes disso, vamos dar uma olhada em outras propriedades da função: as assíntotas e as interseções com os eixos.
Vamos começar com as assíntotas verticais. Pra ter uma assíntota vertical, tem que ter algum ponto do domínio que dê problema. Como láááá do passo 1 vimos que o domínio é o conjunto dos números reais, já descartamos logo as assíntotas verticais!
Agora pras horizontais, não tem jeito, só calculando os limites:
Calculando então os limites, temos:
Fazendo L’Hospital, ficamos com:
Então sim, temos uma única assíntota horizontal, e é a reta . Juntando tudo que vimos, conseguimos esboçar o gráfico! O resultado vai ser:
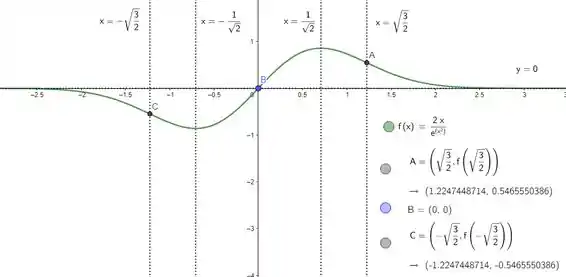
Resposta