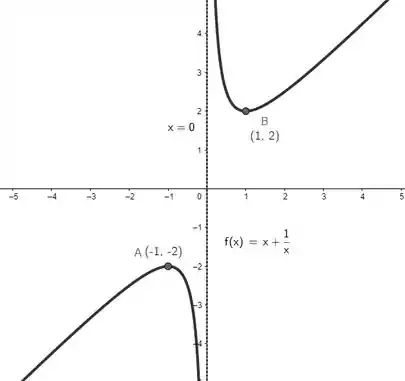
4) Dada a função , explicite o domínio, intervalos de crescimento e decrescimento, concavidade e pontos de inflexão. Finalmente, esboce o gráfico, indicando todos os pontos importantes que você encontrou.
Passo 1
A questão quer da gente bastante coisa a respeito da nossa . Então vamos lá dar pra ela o que ela quer. Vamos começar com o domínio. Vendo bem a nossa função:
A gente vê que não rola! Veja bem, não podemos nem dividir nada por . Sendo assim, o domínio de vai ser:
Vamos ver agora as assíntotas! Começando pelas horizontais, pra gente checar se elas existem, vamos ter que fazer o limite. Então partiu:
Então olha só, não vamos ter assíntotas horizontais! Se a função tivesse, os limites acima teriam dado números. Agora pra ver as verticais, como é um ponto fora do domínio de , ele pode ser um bom candidato à assíntota vertical em! Calculando o limite então:
Opa, então temos sim assíntota! A assíntota que vamos ter é única e vertical e ela vai ser:
Passo 2
Vamos ver agora tudo que envolva a primeira derivada de . Como essa derivada nos dá a inclinação da reta tangente ao gráfico, vai dar pra saber quando a função é decrescente ou crescente e em quais pontos ela troca entre eles. Derivando então:
Beleza. Se a primeira derivada for positiva, a função é crescente. Se for negativa, decrescente. Então vamos igualar à e ver quando isso acontece:
Ok, duas raizes na primeira derivada. Vamos checar o sinal dela então em intervalos que envolvam essa raiz e o domínio de . Os intervalos vão ser:
No primeiro, vamos testar por exemplo. Vamos ter:
No segundo, vamos testar por exemplo. Vamos ter:
No terceiro, vamos testar por exemplo. Vamos ter:
No quarto, vamos testar por exemplo. Vamos ter:
Opa, se antes de a função era crescente e depois se tornou decrescente, o ponto é de máximo e se antes de a função era decrescente e depois se tornou crescente, temos um ponto de mínimo. Resumindo o passo 2, vamos ter:
Passo 3
Bora ver agora a concavidade. Pra isso, a gente vai precisar derivar de novo, beleza? A segunda derivada vai ser então:
E olha só! Como no numerador não temos nenhuma função de , mas no denominador temos um elevado a um número ímpar, vamos ter que:
Ou seja:
Como não existe nenhum ponto que zere a segunda derivada, não teremos pontos de inflexão! E agora temos tudo pra esboçar o gráfico. Juntanto todas as informações que pegamos, chegamos à:
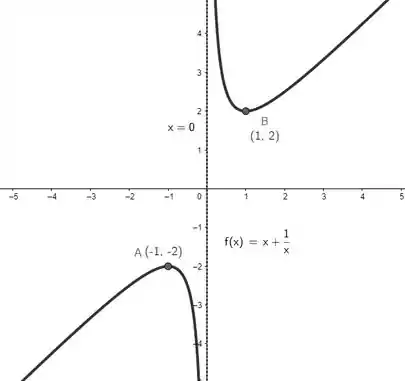
Resposta