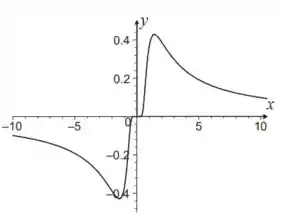
Esboce o gráfico de
Passo 1
Para começar, vamos determinar o domínio da função. A única restrição é para o ponto , pois o denominador se torna nulo. Então o domínio é
Passo 2
Agora, vamos ver se a função tem alguma paridade, ou seja, se ela é uma função par ou uma função ímpar.
- ?
- ?
Não.
Sim.
Passo 3
Agora temos que determinar se a função tem assíntotas. Vamos começar pelas verticais. Essas ocorrem perto de pontos de descontinuidade da função. Nesse caso temos o ponto . Vamos fazer os limites laterais tendendo a esse ponto.
Então a função não possui assíntota vertical.
Agora vamos ver as assíntotas horizontais
Então é assíntota horizontal.
Passo 4
Agora vamos ver crescimento da função. Temos que derivar e ver onde a derivada é positiva e negativa.
Como , o sinal da derivada só será afetado por . Mas veja que também , então, na verdade , o sinal da derivada só depende de . Pelo estudo do sinal de concluímos que a função é decrescente para
e crescente para
Passo 5
Agora vamos determinar os máximos e mínimos da função, se existirem. Primeiro temos que achar os pontos críticos.
Como a derivada muda de positiva para negativa em , significa que esse é um máximo local da função. Já é um mínimo local da função.
Como
e , podemos afirmar que constitui um máximo absoluto da função. Por outro lado, sabemos que
e . Portanto, é um mínimo absoluto da função.
Passo 6
Estamos quase terminando. Falta estudar a concavidade. Bora fazer a segunda derivada.
Eita! Fazer o estudo de sinal desse negócio vai ser uma tarefa bem difícil, pra não dizer impossível. Então, vamos pular essa etapa e usar as informações que já temos para deduzir a concavidade da função.
Bom, quando a partir de sabemos que a função tenderá a zero, sem nunca realmente chegar a esse valor. Se nesse trecho a concavidade fosse para baixo, alguma hora o gráfico ia cruzar o eixo , contrariando o que foi dito acima. Então, a concavidade aí tem que ser para baixo, pois assim o gráfico não encosta no eixo .
O mesmo raciocínio vale para a partir de , mas nesse caso a concavidade tem que ser para cima a fim de que a função nunca enconste no eixo .
No intervalo
sabemos que a função é crescente, mas não podemos afirmar muita coisa sobre a concavidade, então vamos desenhar da maneira que for mais conveniente de acordo com o resto do gráfico.
Passo 7
O esboço do gráfico fica assim:
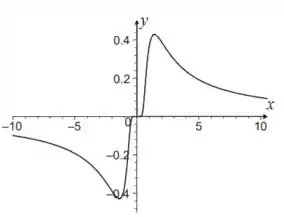
Passo 8
Resposta