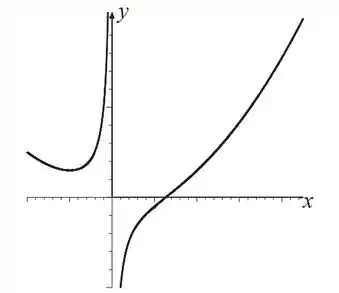
Esboce o gráfico da função e dê explicitamente o que se pede:

• Domínio de
• Paridade de
• Equações das assíntotas verticais e horizontais do gráfico
• Intervalos de em que é contínua
• Pontos de em que a tangente ao gráfico é vertical
• Intervalos de onde é crescente e onde é decrescente
• Extremos relativos de e os respectivos pontos de onde ocorrem
• Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
• Extremos absolutos de e os respectivos pontos de onde ocorrem;
• Imagem de

A função não é par, pois . A função também não é ímpar, porque

As assíntotas verticais ocorrem quando a função se aproxima dos pontos onde o domínio não está definido. Assim,

Portanto, podemos concluir que é assíntota vertical.

Já as assíntotas horizontais, ocorrem com a tendência do limite de no infinito. Usando os limites para , achamos o seguinte:

Ih! Já que os dois limites foram para infinito, a função não tem assíntotas horizontais.

A continuidade da função depende do domínio dela. Onde não existirem descontinuidades no domínio ela será contínua.

Assim, é contínua em .

Os pontos onde a tangente ao gráfico é vertical são aqueles pontos onde a derivada não está definida. Como

então o único ponto em que a derivada não está definida é em . Porém, esse ponto não faz parte do domínio da função, logo não possui pontos em seu domínio onde a tangente é vertical.

Para definir se a função é crescente ou decrescente, devemos olhar para o sinal de sua derivada: onde ela é positiva, cresce; onde é negativa, decresce. Já temos a derivada:

Agora temos que analisar o sinal da derivada. Note que ele só depende de, pois o denominador é sempre positivo. Vamos primeiro ver quando a derivada é positiva:

Agora quando ela é negativa:

Também temos que analisar o sinal nas proximidades de , pois é onde a derivada não existe.

Para temos que e para .

Logo,

• decresce no intervalo
• cresce no intervalo

Os extremos relativos são os máximos e mínimos locais. Para achá-los, primeiro temos que determinar os pontos críticos, fazendo .

Nesse caso, temos que apenas satisfaz isso. Como a derivada muda de negativa para positiva nesse ponto, ele é um mínimo local. Nele, vai valer:

Definimos a concavidade de acordo com o sinal da segunda derivada: se for positiva, concavidade para cima; se negativa, para baixo. Vamos calcular a derivada segunda então!

Agora, analisando o sinal, temos que é positiva quando

E negativa quando

Além disso, temos que analisar seu sinal perto do ponto , onde não está definida.

Para temos que e para

Então, resumindo essa análise de sinal em um esquema, podemos ver que

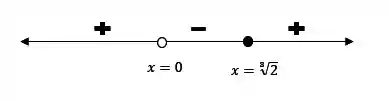
Assim, a concavidade é para cima quando e e para baixo no resto do domínio.

Para pensar em extremos absolutos temos que analisar se os limites da função para são maiores ou menores que os extremos relativos.

No caso, e . Como a função assume valores maiores que ao longo do domínio, então não é mínimo absoluto.

A imagem de consiste em todos os valores que ela pode assumir.

Como ,

Agora juntamos todas as informações para esboçar o nosso gráfico.