USP– Cálculo 1 – Lista 2 – Questão 1.8pParte1
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Passo 1
Oi pessoal, tudo bem por aí? Essa questão nos dá essa função aqui
E pede para esboçar o gráfico das funções e as equações das assíntotas.
E agora, quais informações vamos precisar? Muitas! Por isso nossa resolução vai estar dividida em duas partes! Nessa primeira parte vamos achar os pontos críticos, avaliar os sinais da derivada primeira e segunda e assim determinar pontos de máximo, mínimo e de inflexão, bem como as concavidades.
Beleza?
E depois? Na segunda parte vamos calcular os limites no infinito e determinar os limites em torno dos pontos onde a função não está definida: vamos investigar as ass��ntotas! No fim, juntando tudo isso vamos ter o gráfico da função!
Bora lá!
Passo 2
A primeira derivada da nossa função é
E onde ela é zero
Vamos analisar em torno desse ponto o sinal da derivada
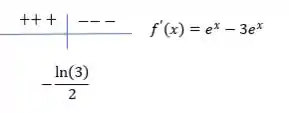
Temos um ponto de máximo em
Beleza?
Podemos ver onde a função é crescente e decrescente:
- Decrescente:
- Crescente:
- Ponto de máximo:
- Côncava para cima:
- Côncava para baixo:
- Decrescente:
- Crescente:
- Ponto de máximo:
- Côncava para cima:
- Côncava para baixo:
Passo 3
Agora vamos analisar a derivada segunda:
Mas nesse ponto vamos verificar a concavidade da função
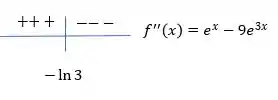
Analisando o sinal da segunda derivada temos que a fiunção é sempre positiva, pois é nosso domínio.
E é isso! Até a parte dois!
Resposta
Resposta
Ei, a resposta está no passo a passo :)