UFES, Sem Campus, Cálculo 1, Listas de Estudos UFES - Cálculo 1 - Lista 11, Questão 5
Nos exercícios a esboce o gráfico da função.
Passo 1
Eaew, tudo certinho contigo?
Temos a seguinte função
queremos esboçar o seu gráfico! Então iremos ter que analisar diversas características! Como, intervalos de crescimento, decrescimento, máximos, mínimos, domínio, quando a função se anula, assim por diante! Vamos ao longo dos passos avaliar tudo que é possível! Vem comigo!
Passo 2
Aqui temos uma função exponencial, que normalmente tem o seguinte formato
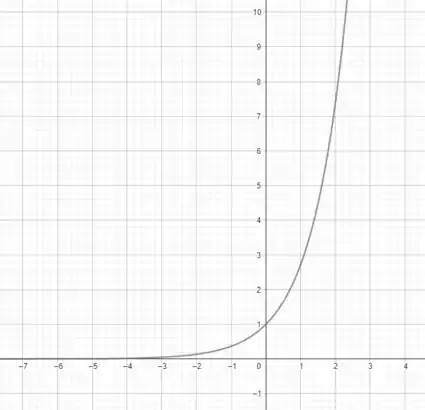
Em particular note que a função cruza o eixo em (), e temos a assíntota dada por
tudo isso é alterado devido às mudanças que foram aplicadas sobre a nossa função! Saca só!
Passo 3
Note que como temos na verdade
a nossa assíntota agora está em
e, quando
Ou seja, o nosso gráfico será espelhado em relação ao eixo ! Mas é só isso que mudou? Nonono! Temos que na vdd, o gráfico é multiplicado por , portanto, o gráfico é espelhado também em relação ao eixo . Além disso, temos que é somada a constante , e sendo assim, o gráfico está levantado, de forma que agora a assíntota está em . O gráfico é da seguinte forma
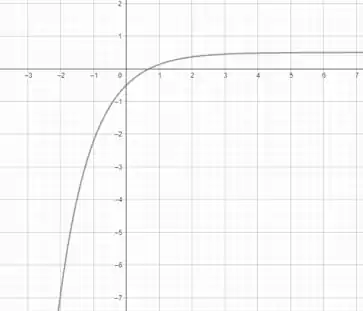
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!