Seguindo o roteiro anterior, esboce os gráficos das funções dadas a seguir.
Passo 1
Fala aí galera, bora resolver o nosso exercício? Bom para resolver, a primeira coisa que precisamos relembrar aqui são as etapas do roteiro:


Show, temos todas as nossas etapas acima e vamos resolver cada uma
Passo 2
- Vamos começar achando o domínio da nossa função:
Reparem que temos uma função e a única restrição é a raiz:
Então
Passo 3
(b) Agora vamos achar as intersecções do gráfico de com os eixos coordenados.
Para acharmos, temos que zerar as variáveis e achar cada componente. Começando por :
Show, achamos valor que o gráfico corta o eixo . Agora vamos
Para sumirmos com a nossa raiz, vamos elevar os dois lados ao quadrado:
Pelo domínio, vimos que , então podemos dizer que
Logo
Passo 4
(d) Agora vamos verificar se o gráfico possui assíntotas.
Vamos começar pela assíntota horizontal. No caso, precisamos calcular o seguinte limite:
Aonde tem que ser um valor inteiro. Vamos lá:
Pelos valores, a função não tem assíntotas horizontais.
Agora partindo para a Assíntota Vertical. No caso, temos que calcular:
Como não temos um ponto, não temos assíntota Vertical.
Passo 5
(e) Encontre os intervalos de crescimento e de decrescimento.
Para isso, temos que começar derivando a nossa função:
Vamos começar definindo quando ela zera:
Para quando é positiva:
Para quando é negativa:
Analisando os valores e o domínio da função:
Passo 6
(f) Encontre os pontos de máximo e mínimo locais.
Para isso, vamos olhar os intervalos achados no Passo anterior:
Reparem que a nossa função vai crescendo, para e começa a decrescer. Então temos ali um ponto Mínimo Local.
Passo 7
(g) Analise a concavidade e encontre os pontos de inflexão.
Vamos começar derivando a nossa primeira derivada:
Agora precisamos analisar quando a nossa segunda derivada é positiva, negativa ou igual a zero.
Vamos começar definindo quando ela zera:
Como temos um valor constante no numerador, a função nunca zera.
Para quando é positiva:
Como é sempre positivo e o numerador também, a relação acima nunca acontece. Então ela não será positiva para todo o o domínio
Para quando é negativa:
Como é sempre positivo e o numerador também, a relação acima sempre acontece. Então ela será negativa para todo o domínio
Analisando os valores e o domínio da função:
Logo, ela só tem concavidade para baixo.
Passo 8
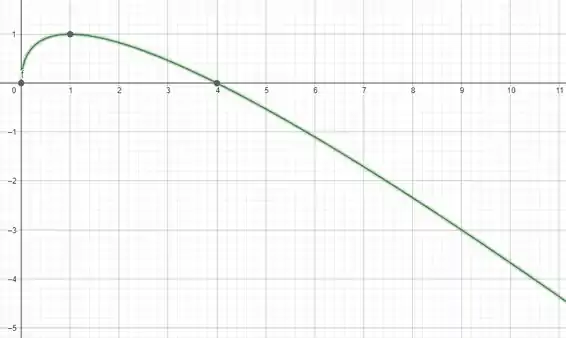
(h) Agora vamos esboçar o gráfico: