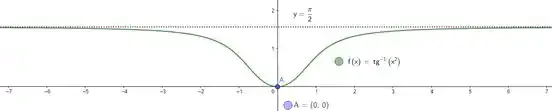
Seja dada por
- Determine s equações das retas assíntotas horizontais do gráfico de , caso existam.
- Determine s equações das retas assíntotas verticais do gráfico de , caso existam.
- Determine os intervalos de crescimento e de decrescimento de .
- Esboce o gráfico de e suas retas assíntotas horizontais e verticais, caso existam. Marque em seu esboço as abscissas dos pontos de máximo e mínimo local de , caso existam.
- Determine todos os valores para os quais a equação possui ao menos uma solução real
Passo 1
Questão completona né? Bora lá começar então. A primeira coisa que a função pede são as assíntotas horizontais. Oras, então basta a gente fazer:
A primeira coisa que a gente tem que notar nesse limite é que e vão dar o mesmo resultado! Veja bem, tem um dentro da função, então tudo que for negativo some, beleza? Vamos ter:
Mas já que a nossa função é uma função trigonométrica inversa, vamos dar uma olhada no círculo trigonométrico pra ver o que acontece nesse limite:
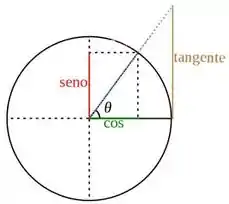
Como queremos o arco cuja tangente é infinita e positiva, temos que ver em qual ângulo a reta vertical do círculo acima é infinitamente grande. E não é que é ? Ou em radianos . Então taí nossa única assíntota horizontal:
Passo 2
Show, vamos ver as assíntotas verticais agora. Pra ter assíntota vertical, temos primeiro que ter algum ponto que “dê problema na função”. Olha só:
Ou seja, não tem nenhum valor de que eu escolha que não me resulte em um . Se olharmos o círculo trigonométrico também:
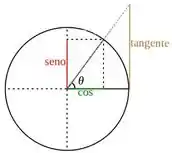
Vemos que realmente qualquer arco que a gente escolha, nos dá um valor possível de tangente. Oras, se o domínio da função é o próprio conjunto dos números reais, não vamos ter assíntotas verticais!
Passo 3
Quando a gente fala de intervalo de crescimento e decrescimento, temos que ver a inclinação da reta tangente, beleza? E quem é essa inclinação se não o valor da primeira derivada em cada ponto?? Temos que derivar então e, só pra lembrar, a derivada de tem um cálculo direto, viu? Vamos ter:
Beleza, mas não é bem que que tá no interior do né? Na verdade, é bem como se tivéssemos:
Opa, se derivarmos nossa , vamos acabar usando a regra da cadeia! Até porque, seja e funções quaisqueres de :
Seguindo essa regra aí, vamos ter:
Agora pra gente ver quando essa derivada é positiva e quando é negativa, vamos ver primeiro quando ela é igual à :
Achamos então a única raíz da derivada! Vamos testar o sinal dela então em intervalos que envolvem essa raíz:
Pro primeiro intervalo, usando, por exemplo, , vamos ter:
Pro segundo intervalo, usando, por exemplo, , vamos ter:
Como no primeiro intervalo a primeira derivada é negativa, a função vai ser decrescente. E como no segundo intervalo a primeira derivada é positiva, a função vai ser crescente. Vamos ter então:
E olha só olha lá! Se antes de chegar em a função decresce e depois cresce, então é um ponto de mínimo! Quando , temos:
Logo o ponto de mínimo tem as coordenadas:
E veja bem, se
Então o ponto de mínimo vai ser um ponto de mínimo global!
Passo 4
Calma gafanhoto, a questão ta acabando. Nesse passo a gente só vai juntar tudo que vimos até agora pra esboçar. Temos:
Juntando isso tudo, a gente consegue ter um esboço, vamos ter:
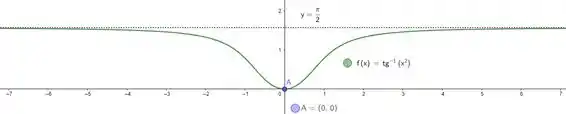
Passo 5
Partiu então fechar a questão com chave de ouro. Temos agora que determinar todos os valores para os quais a equação possui ao menos uma solução real. Mas olha só essa equação como fica se substituirmos :
Ou seja, analisar os valores de é o mesmo que analisar a imagem de , e pelo que já vimos, não passa de e nunca é negativo. Os valores de que fazem a equação possuir pelo menos uma solução real vão ser: