Seja

Faça um esboço do gráfico de explicitando: domínio, pontos críticos (caso existam), intervalos de crescimento e decrescimento, concavidade, pontos de inflexão (caso existam) e assíntotas verticais e horizontais ou oblíquas (caso existam).

Pensando em pontos críticos e crescimento da função a gente tem que observar a derivada primeira desse cara aí:

Temos que o só será nulo quando . Para analisar o sinal de temos que fazer aquele quadro dos sinais clássico, observando que o sinal só depende do e do :

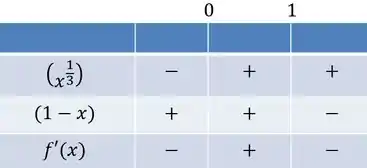
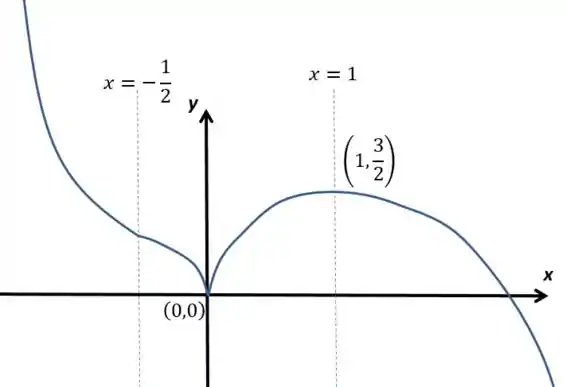
Com isso, a função cresce de até e decresce no resto do domínio. Além disso, é um ponto crítico de máximo, já que a derivada é positiva antes desse número e negativa depois dele.

Pensando agora em concavidade temos que derivar esse cara de novo:

Nem precisamos do quadro de sinais, vendo que será sempre positivo, já que é uma raiz cúbica elevada a um expoente par, no caso. Assim, a concavidade só depende de , e será para cima para todo , para baixo para , sendo esse um ponto de inflexão.

Para as assíntotas, não acharemos nenhuma vertical, já que não existem descontinuidades, como o polinômio tem grau maior que , os limites para também explodirão e não teremos assíntotas horizontais:

Procurando por assíntotas oblíquas teremos a mesma situação, já que o limite da definição do coeficiente angular da assíntota oblíqua também teria problema:

Conclusão, nenhuma, assíntota.

Agora, juntando todas as informações, podemos esboçar o gráfico pedido: