Seja
Pede-se:
.
Intervalos de crescimento e decrescimento, máximos e mínimos locais.
Concavidade e pontos de inflexão.
Assíntotas.
Esboço do gráfico.
Imagem de .
Passo 1
Esse , caso você não conheça a notação, é uma forma escrota de te pedir que derive . Vamos fazer isso então:
Essa é a nossa , acabou letra .
Passo 2
Nós temos, a partir da letra que vale:
Assim, se analisamos o crescimento ou decrescimento de , devemos observar o sinal de . Vamos fazer aquele quadro esperto dos sinais:
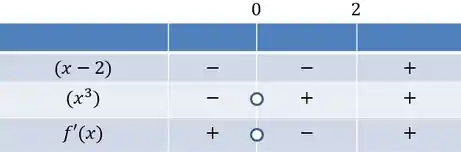
A gente percebe que a região de decrescimento é e de crescimento corresponde ao resto do domínio, ou seja, . Além disso temos que em , o que corresponde a um ponto crítico. Como a derivada é negativa antes e positiva depois esse é um ponto de mínimo local!
Passo 3
Para pensar em concavidade temos que fazer a derivada segunda desse cara aí. O que já temos é:
Agora vamos derivar de novo.
Passo 4
A gente repara que, como o denominador desse termo está elevado a um grau par, ele vai ser sempre positivo. Dessa maneira, o sinal só depende de . Podemos concluir que quando a é negativa e sua concavidade é para baixo. Da mesma forma, quando temos positiva e concavidade para cima. O ponto onde muda essa concavidade é onde temos um ponto de inflexão .
Passo 5
Vamos lançar a assíntota nos limites do domínio. O domínio de por só haver uma restrição fica assim:
Assim, o domínio não tem um limite específico. Vamos observar então o limite de quando para assíntotas horizontais e o ponto da descontinuidade para a assíntota vertical.
Passo 6
Assim, tanto para quanto para temos uma mesma assíntota horizontal: .
Já na descontinuidade temos uma assíntota vertical!
Passo 7
É bom relembrarmos do que achamos nas outras letras:
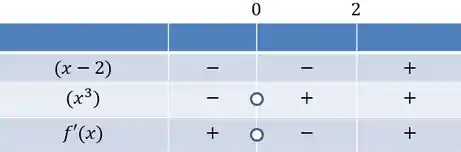
Passo 8
O sinal só depende de . Podemos concluir:
Passo 9
Assim, tanto para quanto para temos uma mesma assíntota horizontal: .
Já na descontinuidade temos uma assíntota vertical!
Passo 10
Agora o gráfico, sabendo que e , fica assim:
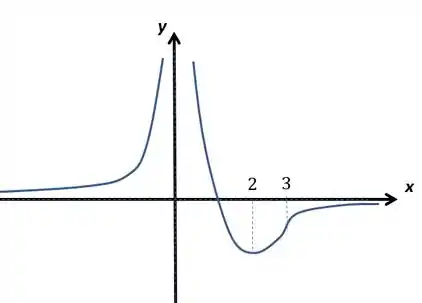
Passo 11
Pelo gráfico, notamos que é mínimo global, o que faz com que a imagem de seja: