Trace o gráfico de uma função contínua y = f (x), tendo todas as seguintes propriedades:
(b) f ′ (x) > 0 para x 0;
Passo 1
Eaew, belezinha?
Temos que traçar o gráfico de uma função contínua que possui as seguintes propriedades:
f ′ (x) > 0 para x 0;
Vamos encontrar uma função que passe por esses pontos. Então vamos lá!
Passo 2
Temos que quando a derivada é positiva, a função é crescente, e quando a derivada é negativa, a função é decrescente. Então, temos uma função crescente para x 0.
Com esse informação, podemos utilizar a função do item anterior, pois ela obedece essas condições:
Então, temos que
f ′ (x) > 0 para x 0;
Passo 3
Traçando o gráfico de :
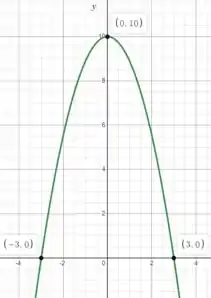
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
No decorrer da questão.