Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Cilíndricas

Ver Teoria
Exercício 38123456789101112131415161718192021222324252627282930313233343536373940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

UFCG – Cálculo 3 – Listas Moodle – 2022/1

3) Arraste e solte, nos campos correspondentes, o valor correto de cada elemento, conforme as opções disponíveis.

b) ∫ 0 3 ∫ 0 1 ∫ 3 ⋅ y 3 cos ⁡ x 2 z d x d y d z = ∫ a b ∫ c d ∫ e f ? ? ? d r d θ d z , onde:

a = ? ? ? ,   b = ? ? ? ,   c = ? ? ? ,   d = ? ? ? ,   e = ? ? ? e f = ? ? ? ;

Passo 1

Falaa... tudo bem???

Nessa questão, repara que já apareceu um r e um θ ali... então nós vamos passar essa integral tripla pra coordenadas cilíndricas.

Lembrando que:

x = r cos ⁡ θ

y = r sen ��� θ

z = z

E não podemos esquecer do Jacobiano, heim!?

J r , θ , z = ∂ x ∂ r ∂ x ∂ θ ∂ x ∂ z ∂ y ∂ r ∂ y ∂ θ ∂ y ∂ z ∂ z ∂ r ∂ z ∂ θ ∂ z ∂ z

E a integral tripla fica:

∫ ∫ ∫ f x , y , z   d x d y d z = ∫ ∫ ∫ J r , θ , z f r , θ , z   d r d θ d z

Passo 2

Como o z não muda, então a = 0 e b = 3 .

Quando usamos coordenadas cilíndricas é como se desenhássemos um cilindro na nossa região. Como o z não está mudando, é como se víssemos o cilindro de cima, então, um círculo:

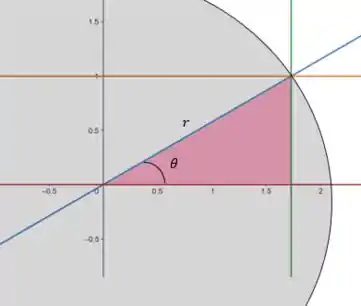
Repara que o r vai variar de r = 0 até a reta verde, né? que é a reta y = 3 :

Mas temos que y = r sen ⁡ θ :

r sen ⁡ θ = 3

r = 3 sen ⁡ θ

r = 3 csc ⁡ θ

Já o ângulo a gente vê que ta mudando de θ = 0 até a reta azul, que é x = 3 ⋅ y

Como x = r cos ⁡ θ e y = r sen ⁡ θ :

r cos ⁡ θ = 3 r sen ⁡ θ

sen ⁡ θ cos ⁡ θ = 1 3

tan ⁡ θ = 3 3

θ = π 6

Passo 3

Não esquecendo do Jacobiano...

J r , θ , z = ∂ x ∂ r ∂ x ∂ θ ∂ x ∂ z ∂ y ∂ r ∂ y ∂ θ ∂ y ∂ z ∂ z ∂ r ∂ z ∂ θ ∂ z ∂ z

= cos ⁡ θ r sen ⁡ θ 0 sen ⁡ θ - r cos ⁡ θ 0 0 0 1

= r

Precisamos mudar o que tem dentro da integral também...

cos ⁡ x 2 z = cos ⁡ r 2 cos 2 ⁡ θ z

Então, a integral fica:

∫ a b ∫ c d ∫ e f ? ? ? d r d θ d z = ∫ 0 3 ∫ 0 π 6 ∫ 0 3 csc ⁡ θ r cos ⁡ r 2 cos 2 ⁡ θ z d r d θ d z

Resposta

∫ 0 3 ∫ 0 π 6 ∫ 0 3 csc ⁡ θ r cos ⁡ r 2 cos 2 ⁡ θ z d r d θ d z

Exercícios de Livros Relacionados

Identifique a superfície de acordo com a equação dada. r = 2 s e nθ
Esboce o sólido descrito pelas desigualdades dadas. 0 ≤ r ≤ 2 ,- π 2 ≤ θ ≤ π 2 ,0 ≤ z ≤ 1
Identifique a superfície cuja equação é dada. 2 r 2 + z 2 = 1
Descreva em palavras a superfície cuja equação é dada. θ = π 4
Marque o ponto cujas coordenadas cilíndricas são dadas. A seguir, encontre as coordenadas retangulares do ponto. ( 1 , π ,e ) ( 1 , 3 π / 2 ,2 )