Calcule as seguintes integrais:
c) , onde é o sólido limitado pelo cilindro , pelo cone e contido no semiespaço .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular a integral tripla na região , que é limitada pelo pelo cilindro , pelo cone e contido no semiespaço . Seria isso aqui:
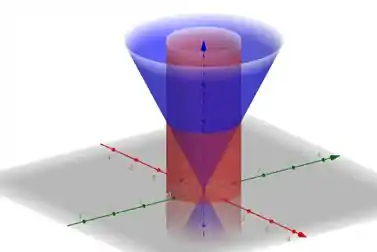
Repare que a região tá dentro do cilindro e entre o plano e o cone. Então, vamos precisar usar as coordenadas cilíndricas pra facilitar nossa vida. Lembra delas? Elas são dadas pelas relações:
Então, vamos analisar o enunciado e traduzir as informações que ele nos deu em coordenadas cilíndricas.
Vamos lá!
Passo 2
Vamos primeiro traduzir a informação de que a região está dentro do cilindro , usando e :
Como , temos:
Agora sabendo que a região está entre o plano e o cone , temos:
E como não temos nenhuma restrição para o ângulo, temos:
Passo 3
Substituindo os limites de integração, vamos ter:
Integrando em relação a :
Integrando agora em relação a :
Antes de integrar em relação a , vamos usar a identidade :
Integrando agora:
Aplicando os limites de integração:
Valeu, galera! Até a próxima! 😉