Questão 4: Determine o volume do sólido limitado superiormente pelo plano , inferiormente pelo plano e lateralmente pelo cilindro .
Passo 1
Bem, um volume de um sólido a essa altura do campeonato é dado pra gente como sendo a integral tripla...
Veja que então basicamente o que temos que fazer é descrever o sólido e depois é só integrar mesmo!
Passo 2
Para descrever o sólido, nada melhor que desenha-lo primeiro só para a gente ter aquela malandragem na hora de descrevê-lo. Como o problema mesmo fala, o sólido está no interior do plano com o plano (acima do plano )...
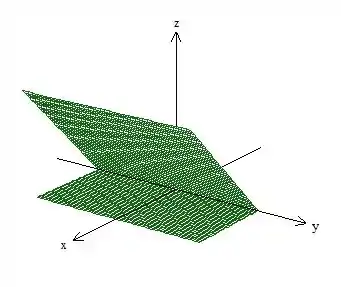
Ele delimita a lateral pelo cilindro de raio ...
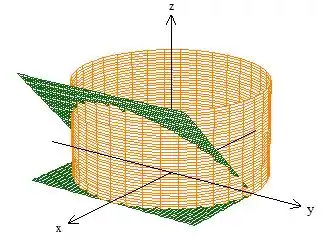
Veja que o sólido basicamente é esse gomo aqui:
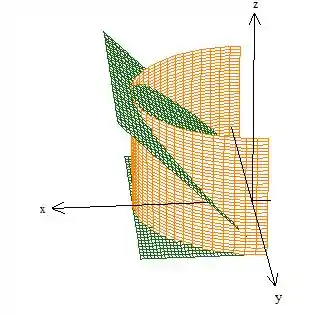
Passo 3
Se estamos trabalhando dentro de um cilindro, nada mais justo que utilizarmos as coordenadas cilíndricas:
O Jacobiano dessa mudança é...
Passo 4
Toda vez que terminamos uma mudança, temos que definir onde as variáveis estão variando. Ou seja, necessitamos de descobrir onde , e variam!
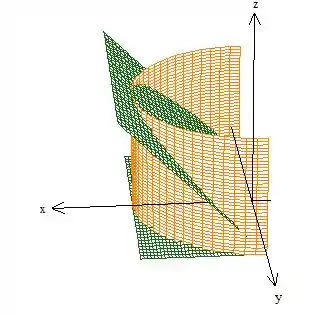
Como é o cara que gira a partir do eixo no sentido anti-horário positivo, vemos que no nosso gomo ele precisa começar negativo e girar até positivo, completando ...
O , varia de até , que é o raio máximo delimitado pelo cilindro...
Quanto ao ... Bem, sabemos que varia de até o plano...
Trocando o pelas coordenadas cilíndricas...
Passo 5
Agora é só voltar para a integral
Trocar tudo e arrasar! (Não se esqueça de quando realizar a troca pelas coordenadas cilíndricas, multiplicar a função pelo Jacobiano):
Passo 6
Bora calcular a integral de dentro então...
Então a do meio...
Por fim a última integral nos dará como resultado...