A seção reta do interior de uma taça é descrita pela equação , onde corresponde ao fundo da taça e à sua altura
Note: Como a taça tem simetria axial, usamos coordenadas cilíndricas!
(a) Esboce a seção reta e determine sua área;
(b) Determine o volume contido na taça.
Passo 1
Letra (a)
Antes de mais nada vamos tentar entender como é o esboço dessa “taça”, nos eixos cartesianos mesmo.
O enunciado nos deu as informações em coordenadas cilíndricas, certo? Isso aqui
A superfície da taça é dada por , no intervalo de , ou seja, vai de:
Sendo que o raio aumenta conforme a gente aumenta , deu pra imaginar um pouco do esboço? Ele é esse aqui
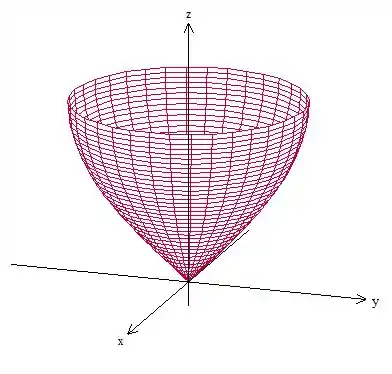
Passo 2
Beleza, mas que tal “seção reta” é essa que o enunciado pede? Como calculo o valor da sua área?
Seção reta nada mais é do que “cortes” dessa taça com plano paralelos ao , por exemplo o plano é esse aqui
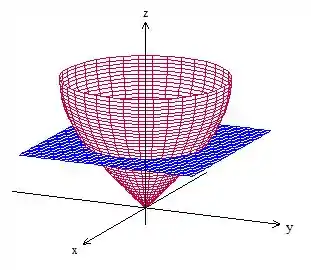
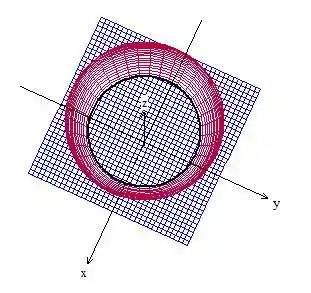
Nesse exemplo aí a minha seção reta é um círculo, sabe qual o raio dele?
Ou seja, pra cada valor de vamos ter uma seção reta como um círculo de raio , sacou isso?
Então qual a área da seção reta?
Bom, essa área depende do valor de , percebe que pra cada vamos ter um raio diferente!
O importante é perceber que todas as seções retas são círculos! E qual a área de um círculo?
O nosso raio depende de , certo? Portanto
Passo 3
Letra (b)
Pra determinar o volume aqui vamos precisar fazer a integral tripla mesmo, não tem jeito.
Só cuidado com o seguinte, queremos o valor dentro da taça, então queremos qualquer raio dentro de , em outras palavras
Os limites de são dados no enunciado
E os limites de são
Justamente porque damos a volta completa pra gerar a taça.
Nós não fizemos nenhuma mudança de coordenadas, mas o enunciado sim! Ele nos deu os dados em coordenadas cilíndricas, então não se esqueça do jacobiano:
Organizando tudo na integral
Passo 4
Bom, vamos integrar isso aí então, começando por
Antes de integrar em , vamos lembrar que
Portanto
Agora sim, integrando em
Por fim, integrando em