Calcule o volume do sólido limitado pelos paraboloides e .
Passo 1
Vamos começar fazendo um esboço da região. Temos dois paraboloides, um virado para cima e que passa pela origem, em vermelho e um virado para baixo (por causa dos coeficientes negativos em e ) e que corta o eixo em :
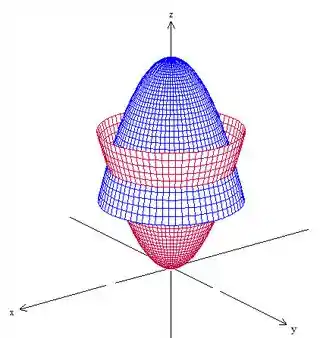
Nós queremos o volume desse sólido, dado por:
Onde é a região limitada pelos paraboloides.
Passo 2
Como o sólido possui simetria em relação ao eixo e as equações que o limitam tem termos quadráticos, vamos usar coordenadas cilíndricas. Faremos:
Passo 3
Vamos, agora, descobrir os intervalos de integração. Substituir esses valores na equação do paraboloide azul:
Para o vermelho:
Como os valores de variam entre o paraboloide vermelho e o azul, temos .
Pelo próprio gráfico, vemos que , faltam, então, os limites de . Já sabemos que , mas qual o seu valor máximo? Temos esse valor quando as duas superfícies se encontram, certo? Vamos, então, fazer essa interseção:
Portanto, descobrimos que . Então, podemos escrever a região como:
Passo 4
Vamos agora substituir os intervalos que encontramos na integral iterada:
Passo 5
Integrando em relação a , temos:
Passo 6
Agora em relação a :
Passo 7
Finalmente, integramos em relação a :