- Calcule , onde é o sólido limitado pelas superfícies e .
Passo 1
Pow! Para começar exercícios como esse, sim, vamos começar como sempre é recomendado: desenhando o sólido ;)
Bem, esse sólido está no interior desse paraboloide ...
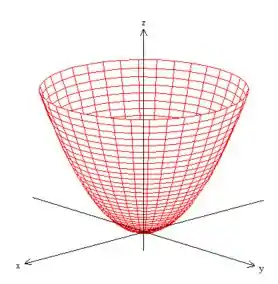
só que está delimitado superiormente por um plano
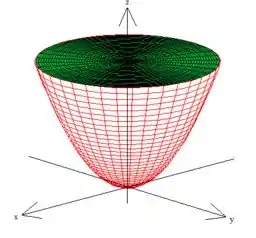
Passo 2
Bem, como estamos trabalhando dentro de uma parabolóide, nada mais legal que pensarmos em uma mudança para coordenadas cilíndricas.
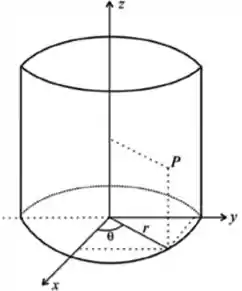
onde vamos trocar
O jacobiano dessa mudança é
E uma equação que nos ajuda, tipo, muuuuuuito é a equação do próprio cilindro:
Nunca devemos sair de uma mudança enquanto não encontramos onde essas novas variáveis estão variando. Bora?
Passo 3
Vamos começar aqui falando do mais fácil: esse ângulo que a esfera dá uma volta completa ao redor do eixo , logo
Quanto ao , bem ele já está um pouquinho mais elaborado, pois se você reparar novamente no sólido, você poderá notar que ele está variando da seguinte forma
ou, em equações...
estamos trabalhando com as coordenadas cilíndricas agora, logo, precisamos trocar esses termos aí
Quanto ao , bem... Venha comigo!
Passo 4
Pow, o está variando em cima do e principalmente de acordo com a mudança, então, não é nada mais justo que olhemos para ó sólido
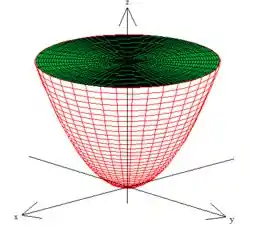
mas dessa vez, de cima para baixo, focando na projeção dele no plano .
Repare que aparentemente, o raio está variando dentro desse círculo aí, certo? Mas não queremos nada mais ou menos e sim certeza. Então repare que esse círculo é formado pela interseção do plano com o elipsoide. Fazer essa interseção é resolver o sistema:
Opa!!! �� de fato uma circunferência com raio , logo
Passo 5
Bem, agora é só montar a integral tripla e correr para o abraço!
Lembre-se de substituir pelas coordenadas cilíndricas e não deixar de multiplicar pelo ;)
Integrando o de dentro e substituindo os limites de integração
Integrando o do meio agora
ganhamos...