Calcule a integral tripla
Onde é a interseção dos sólidos , e
Passo 1
Vamos fazer um esboço da região para entender melhor o que está sendo pedido:
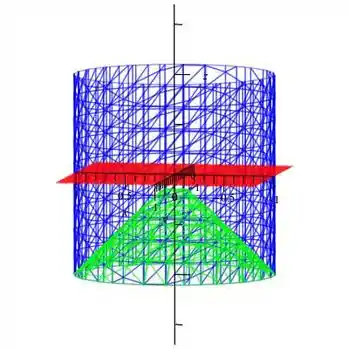
Temos um cilindro de equação , uma folha de cone dada por e o plano limitando (queremos a região abaixo desse plano).
Passo 2
Como o sólido possui simetria em relação ao eixo e as superfícies que o limitam são um cilindro e um cone, vamos usar coordenadas cilíndricas. Faremos:
Passo 3
Vamos, agora, descobrir os intervalos de integração. Fazendo essa substituição na equação do cone, já vimos que temos (com sinal negativo porque estamos nos referindo à folha que tem ). No cilindro, teremos , como também já vimos anteriormente (esse é o valor máximo de , o mínimo é ).
Pelo gráfico, vemos que os valores de variam entre a superfície do cone e o plano , portanto, . Vemos, também, que , uma vez que o sólido está envolta do eixo de simetria . Assim, podemos escrever a região como:
Passo 4
Vamos agora substituir os intervalos que encontramos na integral iterada:
Passo 5
Integrando em relação a , temos:
Passo 6
Agora, integramos em relação a :
Passo 7
Finamente, integramos em relação a :