Calcule a integral tripla.
Onde é delimitado pelo cilindro parabólico e e pelos planos e
Passo 1
Bom dia pra você, estudante mais preparado desse mundão! E se você acha que eu estou mentindo, vem comigo nesse exercício para comprovar que você está sabendo tudo para a sua provinha!
Temos um exercício para calcular uma integral tripla, mas vamos olhar no enunciado quem esse bichão é:
Ótimo, ele me deu a função pra integrar, mas não me deu os limites de integração explicitamente, então não se desespera, vamos olhar para as condições de quem é essa região !
O enunciado me disse que a região é delimitada pelo cilindro parabólico:
E pelos planos:
Olhou para esses planos? Então podemos observar que vai vai de zero até o valor de , então podemos reescrever como
Agora as outras variáveis analisamos em uma região do plano. Colocando no plano e , temos a seguinte imagem:
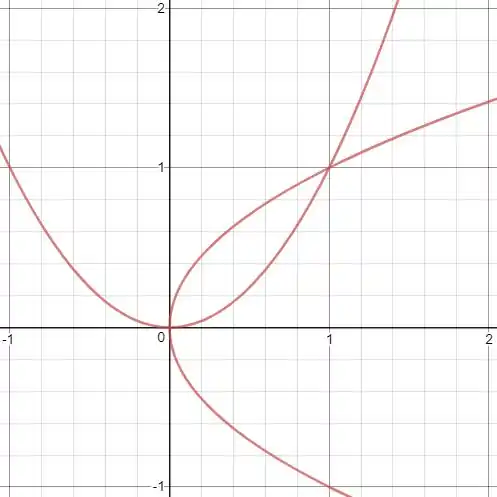
Como os valores de variam de a :
E o valor de é:
Então podemos observar que o valor de irá variar dentro do intervalo:
Temos os intervalos de integração:
Agora sabemos que podemos reescrever a integral que temos que resolver como:
Presta bem atenção na ordem de integração, como o valor de depende de e de , então vamos fazer a integração dele primeiro, depois como o valor de varia com o valor de vamos fazer a integração dele e por último, vamos integrar o valor de que tem os limites de integração como valores numéricos!
Show de bola? Então vamos começar as integrações!
Passo 2
Começando pela integração do valor de , como nossa integral não tem valor nenhum de , vamos considerar que todo o resto é constante:
Fazendo a substituição dos limites de integração, nós temos:
Logo, nossa integral se torna:
Aplicando a distributiva dentro da integral, nós temos:
Passo 3
Vamos continuar a partir da integral em relação a :
Vamos considerar que tudo que não é é uma constante e integrar as parcelas que se somam individualmente:
Substituindo os valores do intervalo de integração em :
Resolvendo isso:
Não precisa resolver mais do que isso, vamos retornar essa expressão feia do jeito que está para nossa integral:
Passo 4
Agora é a hora mágica de fazer a última integração, eu sei que você não aguenta mais, mas é indolor, te prometo!
A expressão que temos que integrar é:
Simplificando a expressão antes da substituição dos valores, ficamos com:
Fazendo a substituição dos valores do intervalo de integração:
Nossa integral se resulta em:
Logo, a integral tripla tem como resultado: