Calcule
Onde é a região do espaço limitada lateralmente pelo cilindro , superiormente pelo plano e inferiormente pelo paraboloide
Passo 1
Vamos começar fazendo um esboço da nossa região , ela é composta por um cilindro com uma tampa plana em cima e um paraboloide em baixo, olha só
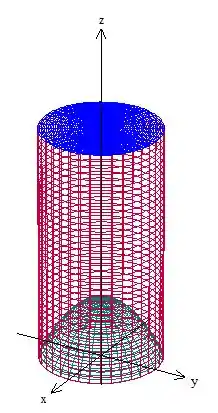
Tanto o paraboloide quanto o cilindro possuem o termo , certo? Deve ajudar bastante utilizar coordenadas cilíndricas aqui então. Vamos fazer essa mudança!
Vemos que o limite inferior de é o paraboloide e o superior é o plano , por isso
Os limites de são:
Projetando tudo isso no plano temos um círculo de raio
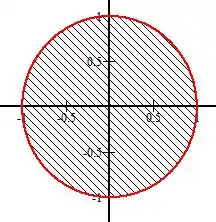
Com isso,
Passo 2
Antes de juntar tudo na integral, vamos ver como fica a função que precisamos integrar
Pronto! Agora sim vamos colocar tudo na integral, não se esqueça do jacobiano
Passo 3
Agora é só integrar! Vamos começar aqui em relação a
Integrando em relação a
Por fim, integrando em relação a