- Use uma integral tripla para calcular o volume do sólido limitado por:
-
e , situado no interior do cilindro , .
Passo 1
Cara! Calculo de volume a esse altura do campeonato pra gente é uma integral tripla de :
Não temos uma boa visualização desse sólido por isso sempre é bom começar por aqui :
O sólido está no interior desse cilindro de raio , e acima do plano
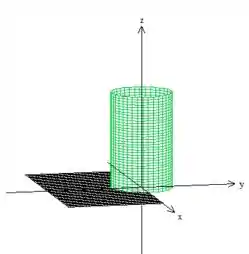
Além disso, o lado direito do cilindro está sendo cortado pelo plano (apenas o lado direito, porque do lado esquerdo ele passa por baixo)
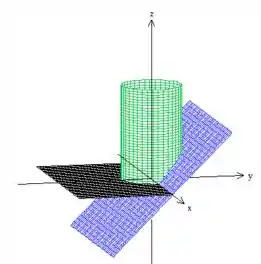
Em cima, por fim, o cilindro é delimitado por esse paraboloide com a boca pra baixo, pois o negativo está no e no :
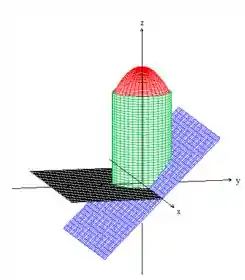
Eis o só lido !
Passo 2
Não trabalhamos com esse sólido dessa forma, por isso, a ideia aqui sempre será partir para a descrição dele. Estamos trabalhando dentro de um cilindro então não é nada mais justo que utilizemos as coordenas cilíndricas:
Uma equação útil é a da circunferência
Passo 3
É necessário que descrevamos onde cada uma dessas variáveis está variando. No caso do , ele deve estar variando de uma “base” até um “teto”.
Porém! Preciso que você note que será necessário repartir a descrição em duas partes, pois em um lado do sólido, o varia da base do plano escuro até o paraboloide e no outro ele começa da rampinha azul, que é o plano . Veja as duas setinhas pretas mostrando esse fato:
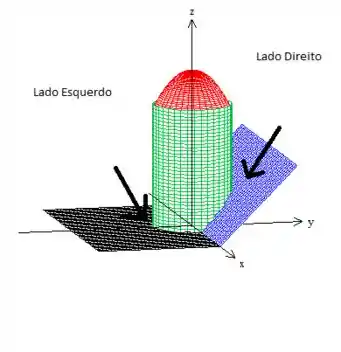
Então, no lado esquerdo:
e do lado direito:
Passo 4
Precisamos também de definir a variação do raio e também do :
No lado direito
O raio varia de até o raio máximo que é o raio do cilindro verde
Enquanto que o inicia sua volta no zero e dá uma meia volta até o fim do lado direito(no lado que você não está enxergando):
No lado esquerdo
o raio continua com a mesma variação
Porém o ângulo , continua onde parou e termina o ciclo de uma vota completa
Passo 5
Concluímos então que teremos, devido essa divisão, que montar duas integrais para o calculo do volume:
No Lado Direito
onde ganhamos a integral tripla (não esqueça de multiplicar a função pelo Jacobiano quando realiza a mudança ):
No Lado Esquerdo
montando essa integral...
O volume de tooodo o sólido que procuramos será então...
Bora calcular essas integrais aí e matar o problema? :D
Passo 6
Vamos de Lado Esquerdo primeiro:
substituindo o Jacobiano...
Calculando a de dentro
Substituindo em ...
e terminando a integral, obteremos...
Passo 7
Vamos de Lado Direito primeiro:
substituindo o Jacobiano...
Calculando a de dentro
Substituindo em ...
substituindo os limite de integração em ... Cuidado para não substituir em !
integrando em e substituindo...
Passo 8
Duas partes de volume calculadas separadas, uma do lado direito e a outra do lado esquerdo, se queremos o volume total, basta somar: