Sabendo que a densidade em qualquer ponto é proporcional à distância do ponto ao eixo z,
determine a massa do sólido cortado do cilindro espesso pelo cone e delimitado inferiormente por .
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou traduzir para você!
O problema começa dizendo que a densidade em qualquer ponto é proporcional à distância do ponto ao eixo z: aqui ele está nos dando indiretamente (como ela se comporta ponto a ponto) como é a densidade de um sólido (que mais tarde ele vai perguntar qual é a massa)
Aí depois ele já fala: calcule massa do sólido: integral! Mas integrar o que? Segue lendo comigo...
E sólido é o resultado do corte (ou seja, da região compreendida) entre o cilindro espesso (aqui a dica é usar coordenadas cilíndricas, já que temos um cilindro... e espesso queremos mesmo o volume de tudo, não só a parte oca) de equação
E pelo cone
E delimitado inferiormente pelo plano , ou seja, por .

Então a ideia aqui é a partir das informações que o problema deu encontrar uma forma para a densidade do material e encontrar também a região no espaço que delimita seu volume . Aí para calcular a massa de qualquer corpo vamos usar que
Mas calma, vou fazer passo a passo com você!
Passo 2
Nossa primeira missão é encontrar a forma da densidade. O problema nos diz que ela é proporcional à distância de um ponto até o eixo , vamos ver como fica isso graficamente?
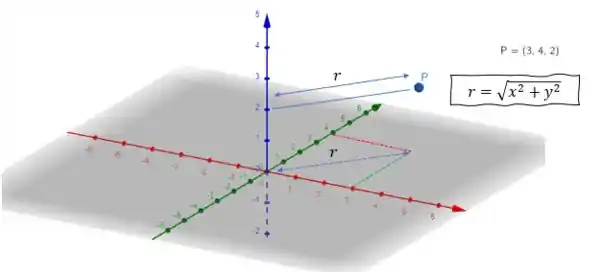
Vamos analisar um ponto qualquer como mostrado ali em cima. Sua altura em relação ao eixo não contabiliza para o cálculo da distância, já que queremos a menor distância entre o ponto P e o eixo z. Por isso podemos projetar a distância de no plano (em cinza) e ver que forma um triângulo retângulo com as projeções das ordenadas x e y

Aí podemos dizer que nossa densidade é:
Aquele k é só uma constante de proporcionalidade, já que o problema não falou nada, podemos assumir que é uma constante qualquer
E já vou colocar em coordenadas cilíndricas, pois nossa integral vai estar nesse tipo de coordenada:
Tranquilo até aqui?

Beleza?
Passo 3
Agora vamos determinar qual é a região desse sólido!
Temos um cilindro bem definido no espaço:
E sabemos que em coordenadas cilíndricas , assim conseguimos encontrar os limites para :
E lembrando que um cilindro é redondo (assim como o cone) então o ângulo vai variar
Beleza?

Agora vamos olhar para o cone! Falta identificarmos os limites para ! O cone tem a seguinte equação:
E em cilíndricas:
E ele é delimitado inferiormente por , então
Bem mais simples né?

Vamos integrar essa coisa agora?
Passo 4
Agora vamos montar e resolver a integral!
A massa do nosso sólido é:
Sabemos que a densidade é . O diferencial de volume em cilíndricas é
E a região é delimitada por:
Agora é só montar!
Como independem de , podemos trazer aquele direto para a última integral e resolver em conjunto. Agora #partiu resolver?
A massa é:
E por fim

Ufa! Terminamos!
E é isso! Espero ter ajudado!
Até próxima!