Calcule
Onde .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para calcular a seguinte integral dupla:
Onde .
Perceba que a região trata-se de uma região circular. Assim, vale a pena a gente alterar para coordenadas polares!!
Lembrando que nas coordenadas polares, temos:
Assim, para definir os limites de integração, vamos observar o gráfico de :
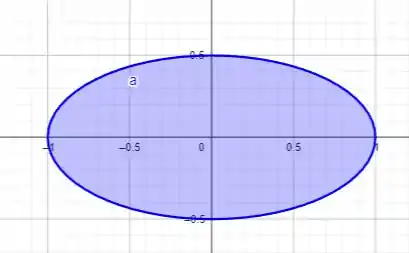
Assim, podemos concluir que:
- varia de a ;
- varia de a .
Assim, temos a nossa integral:
Eaí? Bora lá resolver?
😉
Passo 2
Bom... Integrando primeiro em relação a ,vamos pegar essa integral:
Passo 3
Agora, aplicando o resultado na integral mais externa e resolvendo, temos:
Entendeu direitinho? Responde aee ;)
