3. Encontre a área da parte do paraboloide
Que está acima do plano .
Passo 1
Oi, galerinha! Tudo bom? Aqui nós precisamos calcular a área de uma região. Então vamos começar esboçando ela.
O problema já nos informou que é paraboloide, cuja a equação é:
Ou seja, ele estará ao longo do eixo . Mas o problema, nos deu outra informação, disse que ele é limitado em , ou seja, vamos colocar uma tampa ali. Ficará assim:
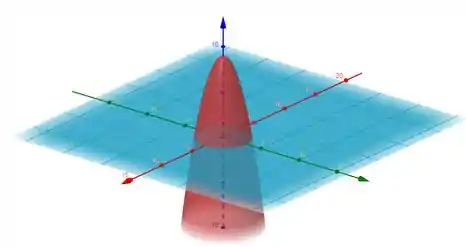
Repara que o plano azul corta o nosso paraboloide vermelho em e temos um topo em .
Agora vamos integrar essa região para achar o volume!
Passo 2
No passo anterior esboçamos a figura, agora precisamos montar a integral para achar seu volume.
Bom, o volume de um sólido pode ser calculado por
Agora olhando para figura vamos delimitar esse região!
Repara que a superfície vermelha é o paraboloide e azul é o plano que limita ela.
Como podemos ver, no plano , temos um domínio . Em , o sólido é limitado embaixo pelo paraboloide e em cima pelo cone . Vamos, então, escrever essa região como tipo I:
Passo 3
Agora precisamos descrever o domínio . Para isso, faremos um esboço da projeção do sólido plano (fazendo a interseção da equação do paraboloide com e olhando de cima):
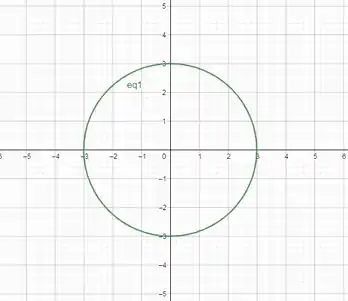
Em a superfície se encontra. Em temos uma circunferência de raio 3. Então, se a projetarmos no plano , teremos a figura acima. Se substituirmos esse valor nas equações das superfícies, encontramos, de fato, .
Como se trata de uma circunferência, vamos escrevê-la com coordenadas polares:
Passo 4
Vamos agora substituir os intervalos que encontramos:
Deixamos para escrever os intervalos de depois para não gerar confusão, pois teremos que fazer a mudança para coordenadas polares.
Integrando em relação a , temos:
Passo 5
Agora vamos descrever a região fazendo a mudança para coordenadas polares (não se esqueça do Jacobiano!). Lembre-se também de que .
Integrando em relação a :
Finamente, integramos em relação a :
Prontinho!