Calcule a massa do sólido dado por
Com densidade
Passo 1
Para calcular a massa vamos precisar da seguinte integral:
Vamos então ter que descobrir os limites de integração de , certo? O esboço é esse aqui:
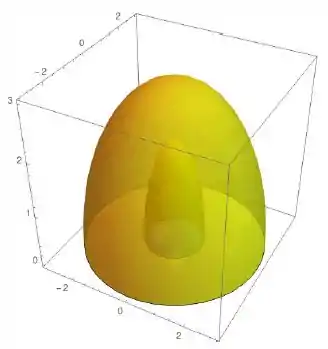
Passo 2
Dá pra ver que o termo aparece em todas as equações apresentadas no enunciado, né? Vamos fazer uma mudança de coordenadas cilíndricas então, vai facilitar muito nossas contas:
Substituindo isso nas nossas superfícies vamos ter que, para a esfera:
E para o elipsoide:
Passo 3
Percebe que vamos ter que dividir nossa região em duas aqui, não tem como fugir disso nessa questão. Em um momento o sólido varia entre e a esfera e em outro momento varia entre o elipsoide e a esfera.
Esse momento aqui tem uma sacada, presta atenção nisso aqui! Nossa integral, substituindo as novas variáveis na densidade e acrescentando o jacobiano fica assim:
Se definirmos os limites de forma a integrar primeiro, como geralmente é feito, perceba que os limites ficariam
Ou seja, não ficaria nada fácil de integrar em depois! Por isso, nessa questão, vamos fazer uma coisa diferente, vamos definir como funções de , é só isolar nas equações da esfera e do elipsoide, fica assim:
Vamos chamar de região aquela que está limitado pelo elipsoide e pela esfera, isso acontece no intervalo de entre e , logo seus limites vão ser:
Por que agora aparece variando entre dois números? Geralmente a gente já faz isso sem perceber até, só que, no jeito mais comum, é o que ficaria variando entre e , por exemplo. No nosso problema, como já definimos variando entre funções de , vai ser que varia entre números!
Vamos fazer o mesmo para a região , já limitamos entre e , falta agora a região em que varia entre e . Nesse caso, olhando pelo gráfico, vemos que o raio varia entre e a esfera. Portanto:
Passo 4
Definidos os limites, vamos reescrever nossa integral:
Passo 5
Integrando em
Da para juntar aqui a segunda integral com parte da primeira! Percebe que aparece limitado por e em nas duas integrais e, em , está limitado por a em seguida por a . Podemos, portanto, juntar esses dois termos em uma só integral que vai de a !
Passo 6
Integrando em
Juntando tudo na mesma integral:
Passo 7
Integrando em