Seja o sólido determinado pelas determinado pelas desigualdades uma unção contínua em e Considere as seguintes afirmações
A(s) afirmação(ões) verdadeira(s) para toda função como acima é(são):
Passo 1
É bom começarmos entendendo a regição que vamos descrever, certo?
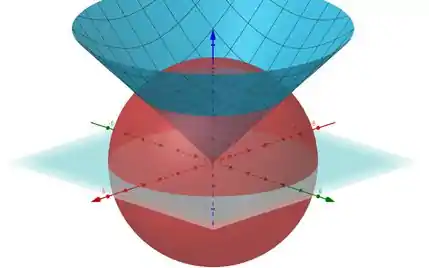
Bom, pra começar vamos aplicar as mudanças propostas pelo próprio enunciado, quando entre todas as opções, ele mostra , beleza?
Então começamos com:
Passo 2
A segunda substituição a ser feita será:
Logo
Passo 3
Agora substituindo a segunda equação na primeira:
Lembrando que o enunciado já nos fala que
Com isso já temos todos nossos intervalos, uma vez que pela imagem você consegue ver que na região que estamos trabalhando (abaixo da esfera e do cone) estamos dando uma volta completa. Logo:
Ficamos então com essa integral!