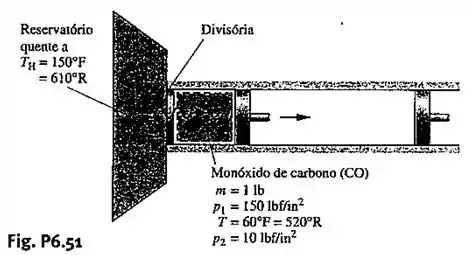
6.51 – Conforme ilustrado na Fig. 6.51, uma parede atua como divisória separando uma libra-massa (0,45 kg) de monóxido de carbono (CO) de um reservatório térmico a 150ºF (65,6 ºC). O CO, inicialmente a 60 ºF (15,6 ºC) e 150 lbf/in2 (1,0 MPa), é expandido isotermicamente até uma pressão final de 10 lbf/in2 (68,9 kPa), enquanto recebe energia sob a forma de calor através da parede do reservatório. O monóxido de carbono pode ser modelado como um gás ideal.
(A) Considerando o monóxido de carbono como o sistema, avalie o trabalho e o calor transferido, em Btu, e a quantidade de entropia gerada em Btu/ºR.
(B) Avalie a produção de entropia, em Btu/ºR, para um sistema estendido que inclua o monóxido de carbono e a parede, considerando que o estado da parede permanece inalterado. Compare com a geração de entropia da parte (A) e comente a diferença.
Passo 1
Antes de começar, você pode iniciar avaliando quais as considerações a se fazer, com base no que foi dito no enunciado.
As considerações que você pode fazer são:
-Modelo de gás ideal para o monóxido de carbono;
-Expansão isotérmica do gás, então a temperatura é constante durante a expansão;
-Sistema fechado, pois se trata de um conjunto cilindro-pistão, pela imagem;
-Sem variação de energia cinética e potencial.
Passo 2
A)
Vamos calcular o trabalho
Para este exercício o sistema é fechado, e a equação do balanço de energia para sistemas fechados é
Onde,
-m é a massa do fluido;
-, é a variação de energia total, em que essa energia total é a soma da energia interna (U), energia cinética (EK) e energia potencial (EP);
-, é a energia interna especifica;
-, é a energia cinética especifica;
-, é a energia potencial especifica;
-Q é o calor transferido;
-W é o trabalho.
Como foi considerado que as variações de energia cinética e potencial são desprezíveis, logo você pode eliminar elas da equação
Como se trata de uma expansão isotérmica, então a temperatura inicial é igual a temperatura final, T1=T2=60ºF.
Vamos relembrar que a variação de energia interna para um gás ideal é função apenas da temperatura, assim como não há variação de temperatura, também não há variação de energia interna
Portanto, o balanço de energia simplifica para essa equação
Você pode lembrar que o trabalho de expansão de um gás pode ser calculado a partir da seguinte expressão
Onde,
-p é a pressão;
-V é o volume;
Em termos de volume especifico
Onde,
-v é o volume especifico;
-m é a massa do fluido;
Passo 3
Você precisar resolver a integral, e para isso precisa achar uma expressão da pressão em função do volume. Como o CO foi considerado um gás ideal, então você pode usar a equação dos gases ideais para achar essa expressão
Onde,
-n é o número de mols;
-R é a constante dos gases ideais que vale 8,314 kJ/kmol.K;
Em unidades de Btu/lbmol.ºR, R vale
Em termos de volume especifico
Onde,
-, é a constante dos gases ideais dividido pela massa molar do gás.
A massa molar do CO é: MMCO=28,0 kg/kmol
Isolando p
Substituindo na integral
Resolvendo a integral
Vamos relembrar que a integral de uma função do tipo , tem a seguinte solução
Assim,
Voltando na equação dos gases ideais, você tem que
Então,
Como T2=T1, então
Passo 4
Calculando o trabalho:
Aplicando os valores
Sendo W=Q, pelo balanço de energia, então
Passo 5
Então, vamos calcular a geração de entropia.
Para a geração de entropia vamos fazer um balanço de entropia, cuja expressão para sistemas fechados é
Onde,
-Q, é o calor transferido;
-Tb é a temperatura da vizinhança;
-ΔS é a variação de entropia;
-σ é a taxa de geração de entropia;
Como Tb é a temperatura da vizinhança, ou seja, é a temperatura nas bordas do sistema. Nessa parte (A) da questão disse para considerar o CO como o sistema. Então por causa disso, você vai usar a temperatura do CO, T=60ºF, como a temperatura da vizinhança, assim
Isolando σ
Passo 6
Para o cálculo da variação de entropia, vamos usar a relação entre a variação de entropia com a pressão e a temperatura, cuja expressão é
Onde,
-ΔS é a variação de entropia;
-, é a entropia especifica de um gás ideal, que depende apenas da temperatura no estado 2;
-, é a entropia especifica de um gás ideal, que depende apenas da temperatura no estado 1;
-, é constante dos gases ideais dividido pela massa molar do gás (no caso, o ar);
Como T2=T1, pois foi dito que a expansão isotérmica, assim você pode fazer a seguinte igualdade
A expressão da variação de entropia fica assim agora
Passo 7
Para o calor, achamos nos passos anteriores que
E W=Q, então
Substituindo
Pela propriedade de Ln
Assim,
Passo 8
B)
Analogamente, na parte (A), para a geração de entropia
Lembrando que Tb é a temperatura da vizinhança do sistema, que é as bordas do sistema, e nessa parte (B) foi considerado pelo enunciado que o sistema inclui a parede a o CO, então a borda do sistema é a parede. Tb então vai ser igual a temperatura da parede (TH)
O processo para determinar a variação de entropia e o calor é análogo ao que foi feito na parte (A), assim
Aplicando os valores
Passo 9
Em comparação com o que foi obtido na questão (A), para a geração de entropia, σ, na questão (B) achamos um valor positivo, isso nos diz que o processo incluindo a parede do reservatório quente no sistema causa irreversibilidades ao processo, enquanto que na parte (A), foi achado um valor nulo para a geração de entropia, isso nos diz que o processo é internamente reversível.
Resposta
A)
B)