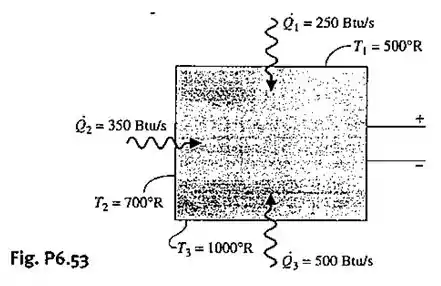
6.53 – Um inventor afirma que o dispositivo ilustrado na Fig. P6.53 gera eletricidade, enquanto recebe calor a uma taxa de 250 Btu/s (263,8 kW) na temperatura de 500ºR (4,6 ºC), uma segunda transferência de calor ocorre a uma taxa de 350 Btu/s (369,3 kW) a 700 ºR (115,7 ºC), e uma terceira a uma taxa de 500 Btu/s (527,5 kW) a 1000ºR (282,4 ºC). Avalie essa afirmativa para uma operação em regime permanente.
Passo 1
Antes de começar, você pode iniciar avaliando quais as considerações a se fazer, com base no que foi dito no enunciado.
As considerações que você pode fazer são:
-Processo em regime permanente, isto é, sem variação das propriedades com o tempo;
-O sistema é aberto, pois temos aqui um processo que envolve taxa;
Passo 2
Nessa questão temos que analisar se a afirmativa de que o dispositivo da figura gera eletricidade é válida, dados os valores de temperatura a calor transferido.
Para isso, você pode usar a entropia para verificar se tal afirmativa é válida.
Vamos relembrar alguns conceitos termodinâmicos para podermos começar a resolver a questão.
Os conceitos que serão úteis aqui são sobre processos reversíveis e irreversíveis, e geração de entropia. Um processo reversível é aquele que é possível retornar ao seu estado inicial, já processo irreversível é aquele em que isso não é possível.
A geração de entropia está diretamente relacionada com esses termos. Quando um processo é reversível a geração de entropia é nula.
Quando o processo é irreversível, a geração de entropia é sempre maior que zero.
Portanto, a geração de entropia é sempre maior ou igual a zero para qualquer processo, caso contrário este processo não pode ocorrer
Passo 3
Então, vamos calcular a geração de entropia do processo.
Você pode calcular a geração de entropia a partir de um balanço de entropia.
Foi considerado que o processo ocorre em um sistema aberto, o que é plausível você considerar isso, pois temos na questão taxa de transferência de calor. Com isso, você vai usar a equação do balanço de entropia para sistemas abertos, cuja expressão é
Onde,
- é a taxa de transferência de calor na posição da fronteira j;
-Tj é a temperatura na posição da fronteira j do sistema;
-, é a taxa de variação de entropia;
-, é a entropia especifica do fluido na entrada do sistema;
-, é a entropia especifica do fluido na saída do sistema;
-, é a vazão mássica do fluido na entrada do sistema;
-, é a vazão mássica do fluido na saída do sistema;
- é a taxa de geração de entropia;
Passo 4
Vamos agora tentar simplificar o balanço de entropia, analisando o processo e as considerações.
Primeiro, você pode notar que não foi informado nada sobre vazões mássicas, isso porque o sistema mostrado na figura P6.53 é um gerador de eletricidade que não possui entrada e nem saída de fluidos, então os termos da vazão mássica da equação do balanço de entropia são nulos.
Pegando a consideração de que o processo está em regime permanente, que diz que nada varia com o tempo, então a taxa de variação da entropia com o tempo é nula.
Assim,
Passo 5
Abrindo o somatório
Agora é só substituir os valores
Passo 6
A avaliação que você pode fazer em relação este resultado é de que, como foi encontrado um valor negativo para a geração de entropia, então o processo nas condições estabelecidas não é possível de ocorrer, pois ele não respeita a 2ª Lei da Termodinâmica. Portanto o dispositivo não gerará eletricidade como foi dito.
Resposta
Processão não é possível de ocorrer.