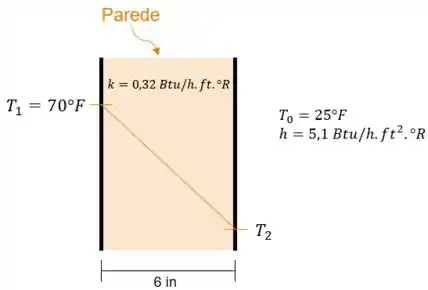
Conforme mostrado na figura abaixo, a parede externa de um edifício tem 6 in (0,1 m) de espessura e possui uma condutividade térmica média de 0,32 Btu/h.ft.°R (0,55 W/m.K). Em regime permanente, a temperatura da parede diminui linearmente de 70°F (21,1°C) na superfície interna para na superfície externa. A temperatura externa relativa ao ar ambiente é = 25°F (23,9°C) e o coeficiente de transferência de calor por convecção é 5,1 Btu/h.ft².°R (29,0 W/m².K). Determine (a) a temperatura , em °F, e (b) a taxa de transferência de calor através da parede, em Btu/h por ft² de área de superfície.
Passo 1
Primeiro vamos considerar algumas hipóteses importantes:
1 – O processo na parede ocorre em regime permanente.
2 – A temperatura varia linearmente através da parede.
3 – A transferência de calor fora da parede acontece somente por convecção.
E agora vamos só dar uma reorganizada nos dados, lembrando da conversão de Fahrenheit para Rankine!
Passo 2
Pela hipótese 3, toda transferência de calor que ocorre por condução dentro da parede, depois passa por convecção para o ar ambiente. Então vamos ter:
Pela hipótese 1 e 2, temos:
Voltando para a primeira equação e substituindo teremos:
Agora é só isolar !
Vamos arrumar só mais um pouquinho tirando esses L dos denominadores:
Bem melhor né? Só substituir os dados na equação:
Passo 3
Pronto! Nós temos a equação:
E na letra (b) é pedido !
Então só substituir os dados e achar a relação: