Uma parede plana composta consiste em uma camada de blocos de betão como isolante, de 12 in (0,3 m) de espessura, sendo = 0,7 Btu/h.ft.°R (0,47 W/m.K) e uma camada de placas de gesso com 0,625 in (0,016 m) de espessura (= 1,11 Btu/h.ft.°R = 1,9 W/m.K). As temperaturas das superfícies exteriores do betão e do gesso são 460 °R (-17,6°C) e 560 °R (38,0 °C), respectivamente, e existe um contato perfeito na interface entre as camadas. Determine, em regime permanente, a taxa instantânea de transferência de calor, em Btu/h por ft² de área de superfície, e a temperatura em °R, na interface entre o betão e o gesso.
Passo 1
Antes de tudo! O que é betão?

É o nosso velho conhecido CONCRETO, mas em português de Portugal!
Agora vamos para a questão mesmo! Começando pelo esquema do sistema:
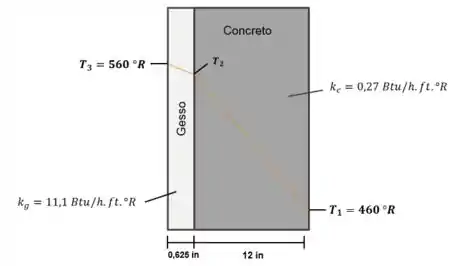
Vamos também levantar algumas hipóteses para a questão:
1 – O processo que acontece nas paredes acontece em regime permanente.
2 – A distribuição de temperaturas é linear em ambas paredes.
3 – As duas paredes estão em contato térmico perfeito, sem perdas.
4 – A condutividade térmica em ambas paredes é uniforme.
E agora os dados:
Passo 2
Pela hipótese 3, toda transferência de calor que ocorre por condução dentro da parede de gesso passa também por condução para a parede de concreto. Então vamos ter:
Pela hipótese 1 e 2, temos:
Para a parede de gesso:
Para a parede de concreto:
Igualando ambas as equações:
Vamos isolar para poder achar seu valor:
Substituindo os dados:
Passo 3
Agora é só substituir o na formula da transferência de calor ou do gesso ou do concreto:
Utilizando a do gesso: