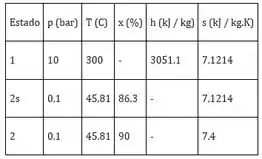
Os dados para a operação em regime permanente de uma expansão adiabática de vapor através de uma turbina estão apresentados na tabela a seguir. Os estados estão numerados, conforme indicado na Fig. 6.11. Os efeitos das energias cinética e potencial podem ser desprezados. Determine para a turbina (a) o trabalho desenvolvido por unidade de massa de capor em escoamento, em kJ/kg, (b) a quantidade de entropia gerada por unidade de massa de vapor em escoamento, em kJ/kgK, e (c) a eficiência isentrópica da turbina.
Passo 1
Simbora lá pra mais uma!
Vamo aplicar um equilibriozinho de energia, teremos:
Reduzindo, teremos:
Com , encontraremos na tabela de vapor que:
Tendo , encontraremos:
Ao substituir, teremos:
Para o estado real 2, tendo , teremos:
Substituindo,
Passo 2
Belê, conseguimos bastante informação! Com elas, conseguimos calcular o trabalho hein, vamo lá:
Para encontrar a quantidade de entropia, teremos:
Substituindo os valores,
Já nossa eficiência isentrópica vai ser dada por:
Resposta
- 705,58 kJ/kg
- 0,279 kJ/kgK
- 88,85%