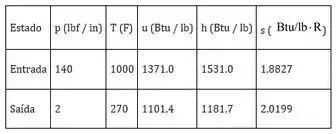
Os dados para a operação em regime permanente de uma expansão adiabática de vapor através de uma turbina, com 4 lb/s de vazão mássica, estão apresentados na tabela a seguir. Os efeitos das energias cinética e potencial podem ser desprezados. Determine para a aturbina (a) a potência desenvolvida, em HP, (b) a taxa de entropia gerada, em HP/°R, e (c) a eficiência isentrópica da turbina.
Passo 1
Simbora lá pra mais uma!
Vamo aplicar um equilibriozinho de energia, teremos:
Reduzindo, teremos:
Temos as entalpias, então, só substituir:
Passo 2
Bora lá, calculando agora a taxa de produção de entropia, teremos:
Passo 3
Ta tabela A-3E, conseguimos encontrar propriedades da água saturada para , teremos:
Calculando o estado ideal, teremos:
Assim,
Calculando a eficiência isentrópica, teremos:
Resposta
- 1976,3 hp;
- 0,77644 hp/R;
- 80%