Ar escoa através de um duto circular isolado com de diâmetro. Os valores da pressão e da temperatura em regime permanente obtidos através de medições realizadas em duas posições, indicadas por 1 e 2, são dados na tabela a seguir. Admitindo o modelo de gás ideal para o ar com , determine:
a) o sentido do escoamento.
b) a velocidade do ar, em , nas duas posições.
c) a vazão mássica do ar, em .
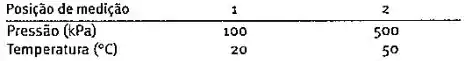
Passo 1
E aí, beleza?
Vem comigo resolver essa questão!
Fica de olho para não se perder!
Letra a)
Começamos o nosso problema aplicando a equação de entropia em nosso sistema:
Como , temos:
Abrindo para um gás ideal:
Substituindo os dados:
Como deve ser sempre maior que 0, temos que o ar flui de 2 para 1.
Passo 2
Letra b)
Aplicando a equação de continuidade:
Como , simplificando a equação:
Substituindo os dados:
Do balanço de taxa energia desprezando os efeitos da energia potencial, temos:
Como , então:
Substituindo :
Substituindo os dados:
Assim:
Passo 3
Letra c)
Por fim, calculando a vazão mássica do ar:
Substituindo os dados:
E fim!
Até a próxima questão!