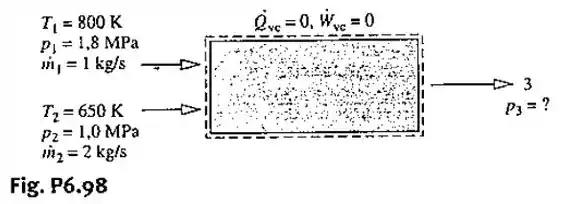
A Fig. P6.98 fornece dados de um teste em regime permanente para um volume de controle no qual entram dois fluxos de ar misturados de maneira a formar um único fluxo de saída. As perdas de calor podem ser desprezadas. Uma cópia desbotada da folha de dados indica que a pressão do fluxo de saída pode ser ou . Admitindo o modelo de gás ideal para o ar com , determine se algum ou ambos os valores de pressão podem estar corretos.
Passo 1
Fala, galerinha!
Se ajeitem aí e bora resolver essa questão juntos!
Começamos o nosso problema aplicando a equação da continuidade em nosso sistema:
Agora, a equação de taxa de energia:
Como , temos:
Abrindo :
Abrindo essa equação:
Isolando :
Substituindo os dados:
Passo 2
Aplicando a equação de taxa de equilibro de entropia:
Como , temos:
Como podemos considerar o gás como um gás ideal, temos:
Substituindo os dados:
Passo 3
Agora, devemos verificar o valor de .
Se :
Como , não podemos aceitar esse valor.
Se :
Como , podemos aceitar esse valor como correto.