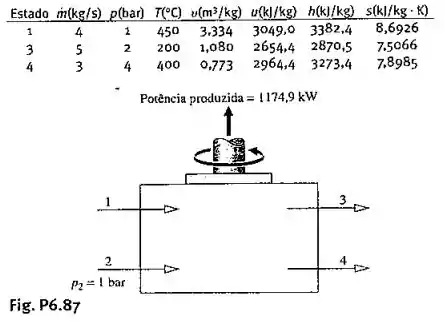
Um inventor afirma que em regime permanente o dispositivo ilustrado na Fig. P6.87 desenvolve potência a partir das correntes de água que entram e saem a uma taxa de . A tabela a seguir fornece dados para a entrada 1 e as saídas 3 e 4. A pressão na entrada é . Considere que as perdas de calor e todos os efeitos das energias cinética e potencial são desprezíveis. Avalie a afirmação do inventor.
Passo 1
E aí, tudo bem?
Vem comigo resolver essa questão!
Começamos o nosso problema aplicando a equação da continuidade em nosso sistema:
Aplicando um balanço de taxa de energia:
Como , temos:
Isolando :
Substituindo os dados:
Passo 2
Como conhecemos os valores da pressão e da entalpia no estado 2, podemos obter os valores de entropia a partir das tabelas de vapor d’água superaquecido:
Aplicando a equação de equilíbrio de entropia em nosso sistema:
Como , então:
Substituindo os dados:
Como a geração de entropia encontrada é negativa, temos então, pela 2ª Lei, que a afirmação do inventor está errada.
Até a próxima questão!